- Tham gia
- 3/7/07
- Bài viết
- 4,946
- Được thích
- 23,213
- Nghề nghiệp
- Dạy đàn piano
Chuyển đổi các đơn vị đo lường với nhau
Sẽ có rất nhiều lúc chúng ta muốn biết 1 inch bằng bao nhiêu centimet, 1 pound nghĩa là mấy ký, v.v... Excel cung cấp cho chúng ta một công cụ để chuyển đổi các đơn vị đo lường, từ hệ đo lường này sang hệ đo lường khác. Đó là hàm CONVERT()
Hàm CONVERT()
Cú pháp: = CONVERT(number, from_unit, to_unit)
Cách nhập chữ viết tắt trong from_unit và to_unit:
number : Giá trị muốn chuyển đổi
from_unit : Đơn vị đo lường gốc (của number) muốn chuyển
to_unit : Đơn vị đo lường cho kết quả chuyển đổi
Cách nhập chữ viết tắt trong from_unit và to_unit:
CONVERT() chấp nhận các giá trị text như sau, khi nhập, phải đặt chúng trong cặp dấu nháy kép, và CONVERT() chỉ chuyển đổi qua lại giữa các loại đơn vị trong cùng một nhóm (Vd: không thể đổi inch sang lít được)
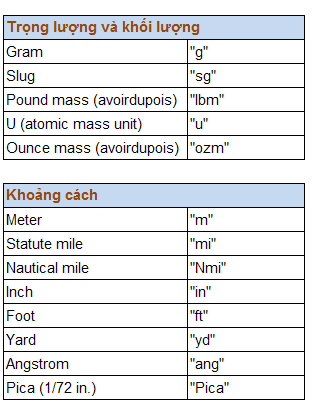
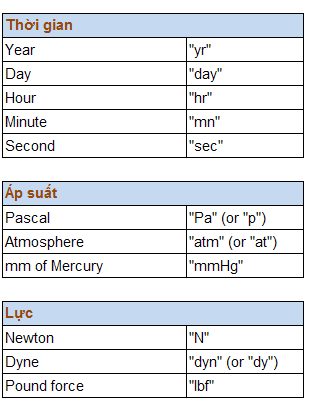
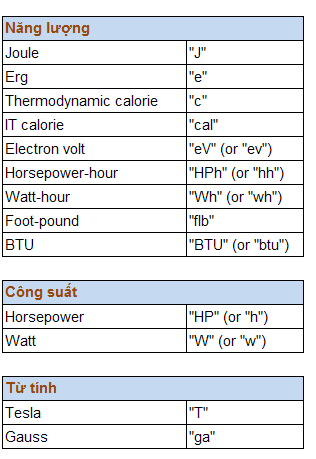
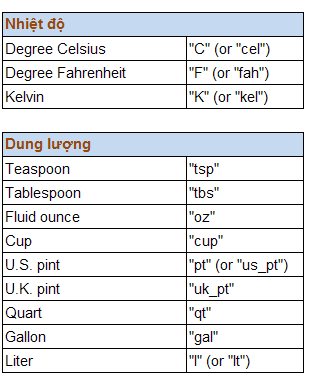 Đơn vị tiền tố (prefix) viết tắt sau đây có thể được chuyển đổi qua lại với nhau. Khi nhập các đơn vị tiền tố viết tắt này, cần phân biệt chữ thường và chữ hoa.
Đơn vị tiền tố (prefix) viết tắt sau đây có thể được chuyển đổi qua lại với nhau. Khi nhập các đơn vị tiền tố viết tắt này, cần phân biệt chữ thường và chữ hoa.
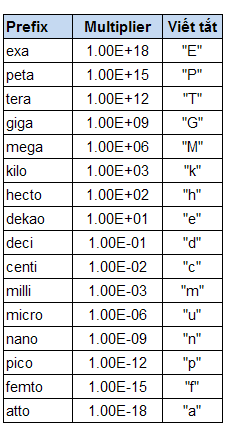
Lưu ý:
Ví dụ:





Lưu ý:
- Nếu loại dữ liệu nhập vào không hợp lệ, hàm sẽ trả về lỗi #VALUE!
- Nếu loại đơn vị không tồn tại, hoặc không hỗ trợ tiền tố (prefix) viết tắt, hoặc không nằm trong cùng một nhóm, hàm sẽ trả về lỗi #NA!
Ví dụ:
CONVERT(1.0, "lbm", "kg") = 0.453592 (1 pound = 0.435392 kg)
CONVERT(68, "F", "C") = 20 (68 độ F = 20 độ C)
CONVERT(2.5, "ft", "sec") = #NA! (đơn vị chuyển đổi không cùng 1 nhóm)
CONVERT(CONVERT(100,"ft","m"),"ft","m") = 9.290304 (100 dặm vuông = 9.290304 mét vuông)
CONVERT(68, "F", "C") = 20 (68 độ F = 20 độ C)
CONVERT(2.5, "ft", "sec") = #NA! (đơn vị chuyển đổi không cùng 1 nhóm)
CONVERT(CONVERT(100,"ft","m"),"ft","m") = 9.290304 (100 dặm vuông = 9.290304 mét vuông)