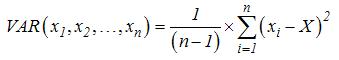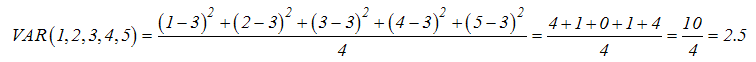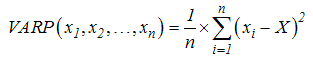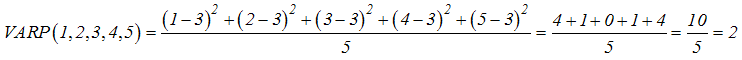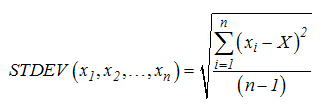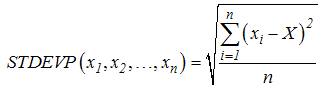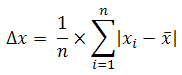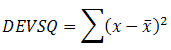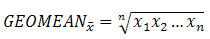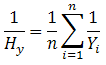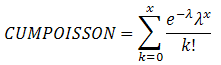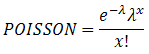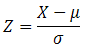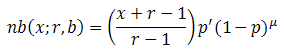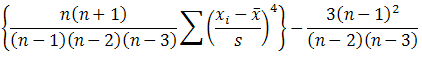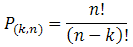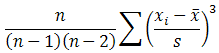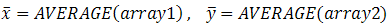- Tham gia
- 3/7/07
- Bài viết
- 4,946
- Được thích
- 23,213
- Nghề nghiệp
- Dạy đàn piano
Phần này được viết tặng riêng các bạn đam mê những bộ môn xác suất, toán thống kê, toán ứng dụng, v.v...
Do kiến thức về thống kê của tôi chỉ có hạn, nên sẽ có những bài tôi chỉ giới thiệu cú pháp hàm và một số ví dụ lấy từ phần Help của Excel 2007, chứ không thể mô tả đầy đủ cách thức sử dụng chúng, vì có một số hàm đòi hỏi người sử dụng phải có một khái niệm tối thiểu nào đó về thống kê, thì mới biết sử dụng chúng. Về những loại "phân phối" trong thống kê, nếu tìm được bài viết nào có liên quan đến chúng, tôi sẽ giới thiệu link để các bạn đọc thêm.
Nhân đây cũng xin giới thiệu bài viết "Tạo bảng tra các phương pháp tính xác suất thống kê trong Excel" của bạn ttphong2007.
Danh mục các Hàm Thống kê
Các hàm thống kê có thể chia thành 3 nhóm nhỏ sau: Nhóm hàm về Thống Kê, nhóm hàm về Phân Phối Xác Suất, và nhóm hàm về Tương Quan và Hồi Quy Tuyến Tính
1. NHÓM HÀM VỀ THỐNG KÊ
-------------------------------------------
2. Nhóm hàm về Phân Phối Xác Suất ...
3. Nhóm hàm về Tương Quan và Hồi Quy Tuyến Tính ...
Do kiến thức về thống kê của tôi chỉ có hạn, nên sẽ có những bài tôi chỉ giới thiệu cú pháp hàm và một số ví dụ lấy từ phần Help của Excel 2007, chứ không thể mô tả đầy đủ cách thức sử dụng chúng, vì có một số hàm đòi hỏi người sử dụng phải có một khái niệm tối thiểu nào đó về thống kê, thì mới biết sử dụng chúng. Về những loại "phân phối" trong thống kê, nếu tìm được bài viết nào có liên quan đến chúng, tôi sẽ giới thiệu link để các bạn đọc thêm.
Nhân đây cũng xin giới thiệu bài viết "Tạo bảng tra các phương pháp tính xác suất thống kê trong Excel" của bạn ttphong2007.
Danh mục các Hàm Thống kê
Các hàm thống kê có thể chia thành 3 nhóm nhỏ sau: Nhóm hàm về Thống Kê, nhóm hàm về Phân Phối Xác Suất, và nhóm hàm về Tương Quan và Hồi Quy Tuyến Tính
1. NHÓM HÀM VỀ THỐNG KÊ
AVEDEV (number1, number2, ...) : Tính trung bình độ lệch tuyệt đối các điểm dữ liệu theo trung bình của chúng. Thường dùng làm thước đo về sự biến đổi của tập số liệu
AVERAGE (number1, number2, ...) : Tính trung bình cộng
AVERAGEA (number1, number2, ...) : Tính trung bình cộng của các giá trị, bao gồm cả những giá trị logic
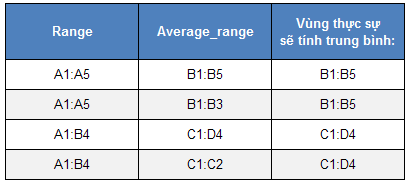
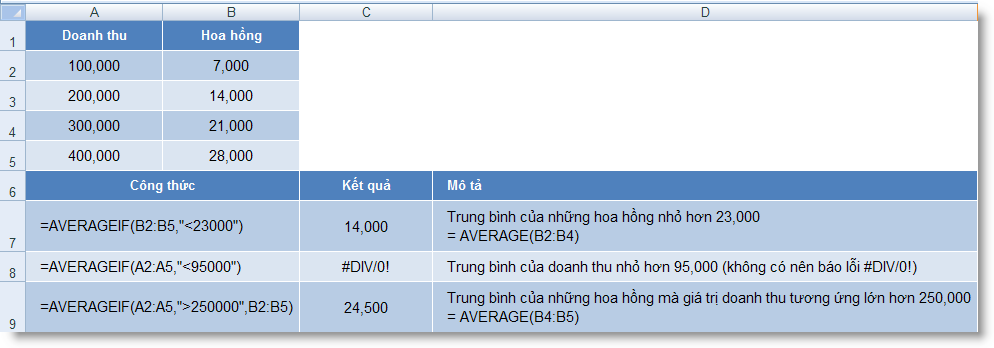
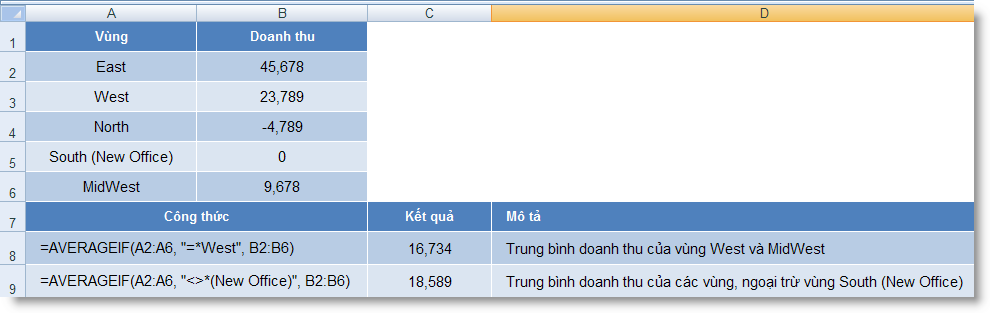
AVERAGEIF (range, criteria1) : Tính trung bình cộng của các giá trị trong một mảng theo một điều kiện
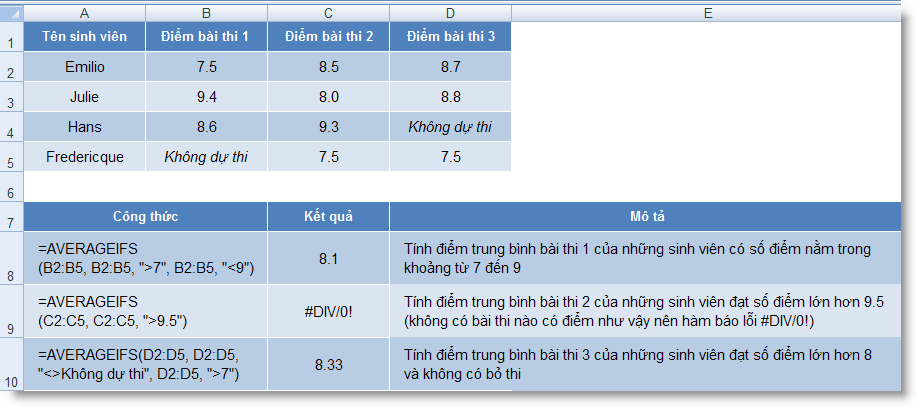
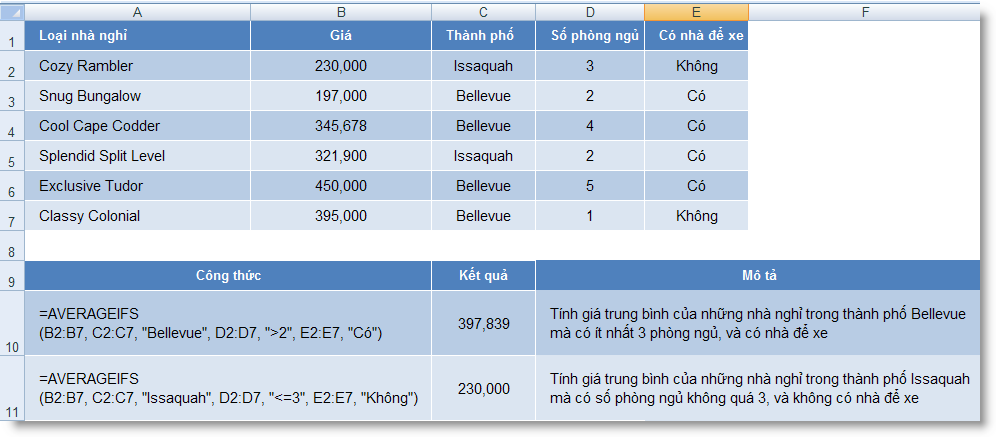
AVERAGEIFS (range, criteria1, criteria2, ...) : Tính trung bình cộng của các giá trị trong một mảng theo nhiều điều kiện
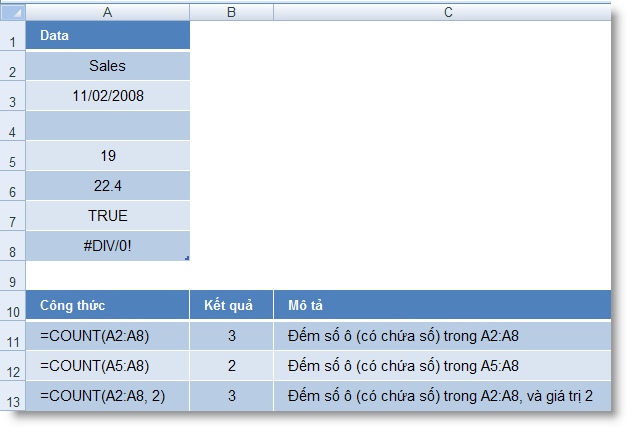
COUNT (value1, value2, ...) : Đếm số ô trong danh sách
COUNTA (value1, value2, ...) : Đếm số ô có chứa giá trị (không rỗng) trong danh sách
COUNTBLANK (range) : Đếm các ô rỗng trong một vùng
COUNTIF (range, criteria) : Đếm số ô thỏa một điều kiện cho trước bên trong một dãy
COUNTIFS (range1, criteria1, range2, criteria2, …) : Đếm số ô thỏa nhiều điều kiện cho trước
DEVSQ (number1, number2, ...) : Tính bình phương độ lệch các điểm dữ liệu từ trung bình mẫu của chúng, rồi cộng các bình phương đó lại.
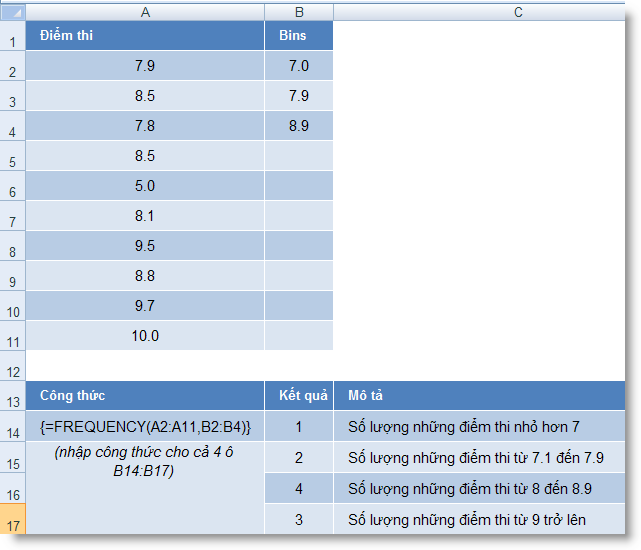
FREQUENCY (data_array, bins_array) : Tính xem có bao nhiêu giá trị thường xuyên xuất hiện bên trong một dãy giá trị, rồi trả về một mảng đứng các số. Luôn sử dụng hàm này ở dạng công thức mảng
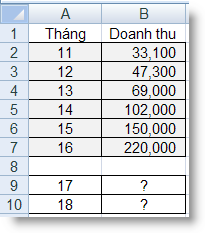
GEOMEAN (number1, number2, ...) : Trả về trung bình nhân của một dãy các số dương. Thường dùng để tính mức tăng trưởng trung bình, trong đó lãi kép có các lãi biến đổi được cho trước…
HARMEAN (number1, number2, ...) : Trả về trung bình điều hòa (nghịch đảo của trung bình cộng) của các số
KURT (number1, number2, ...) : Tính độ nhọn của tập số liệu, biểu thị mức nhọn hay mức phẳng tương đối của một phân bố so với phân bố chuẩn
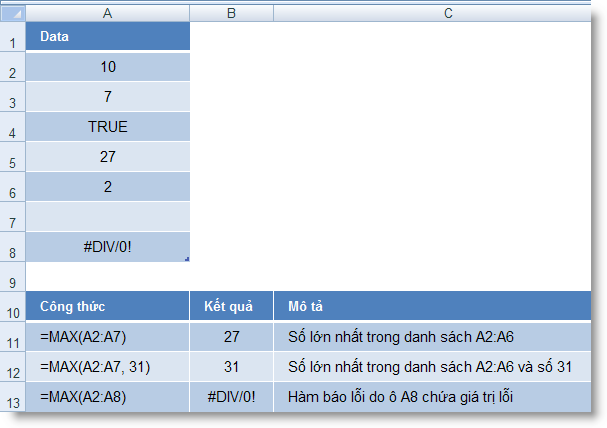
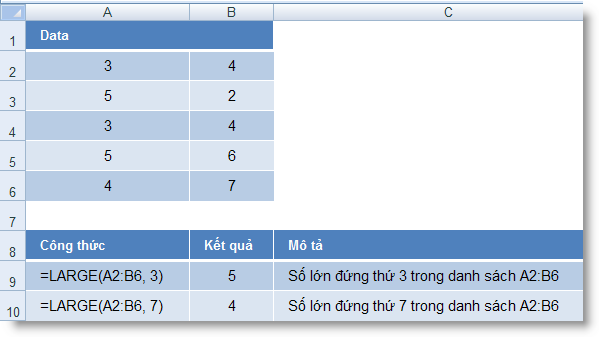
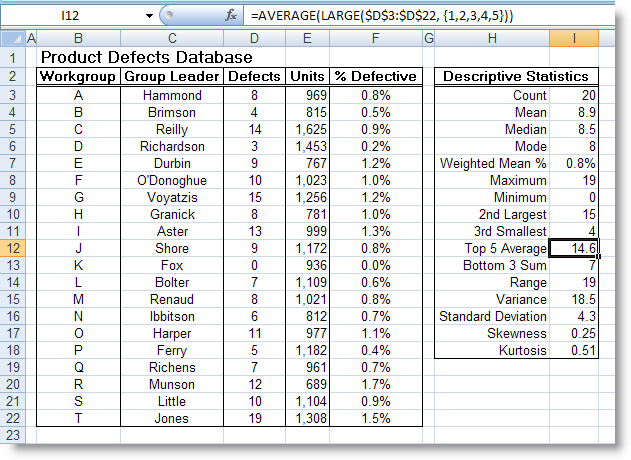
LARGE (array, k) : Trả về giá trị lớn nhất thứ k trong một tập số liệu
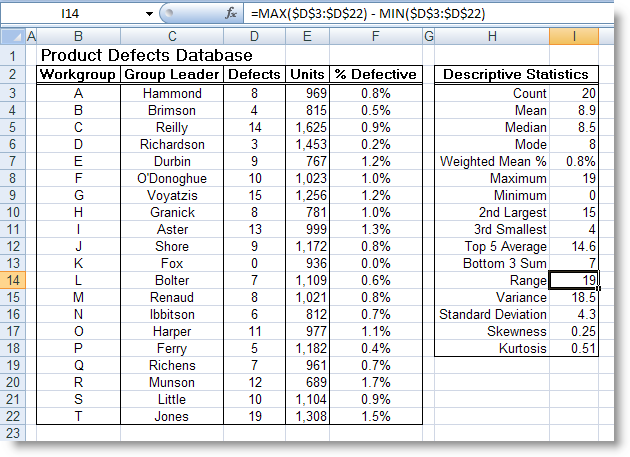
MAX (number1, number2, ...) : Trả về giá trị lớn nhất của một tập giá trị
MAXA (number1, number2, ...) : Trả về giá trị lớn nhất của một tập giá trị, bao gồm cả các giá trị logic và text
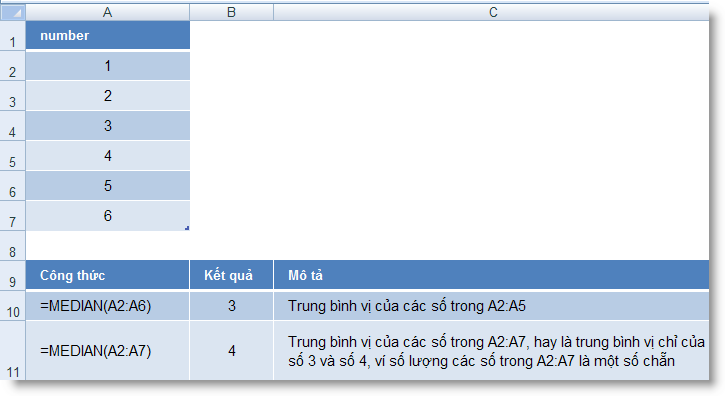
MEDIAN (number1, number2, ...) : Tính trung bình vị của các số.
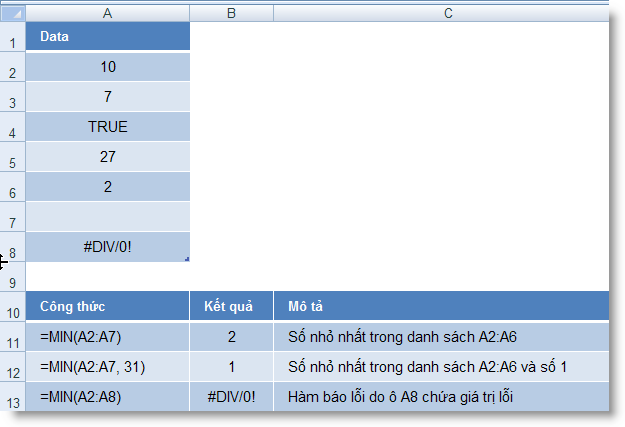
MIN (number1, number2, ...) : Trả về giá trị nhỏ nhất của một tập giá trị
MINA (number1, number2, ...) : Trả về giá trị nhỏ nhất của một tập giá trị, bao gồm cả các giá trị logic và text
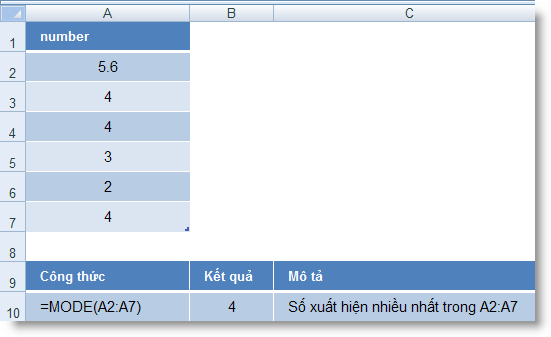
MODE (number1, number2, ...) : Trả về giá trị xuất hiện nhiều nhất trong một mảng giá trị
PERCENTILE (array, k) : Tìm phân vị thứ k của các giá trị trong một mảng dữ liệu
PERCENTRANK (array, x, significance) : Trả về thứ hạng (vị trí tương đối) của một trị trong một mảng dữ liệu, là số phần trăm của mảng dữ liệu đó
PERMUT (number, number_chosen) : Trả về hoán vị của các đối tượng.
QUARTILE (array, quart) : Tính điểm tứ phân vị của tập dữ liệu. Thường được dùng trong khảo sát dữ liệu để chia các tập hợp thành nhiều nhóm…
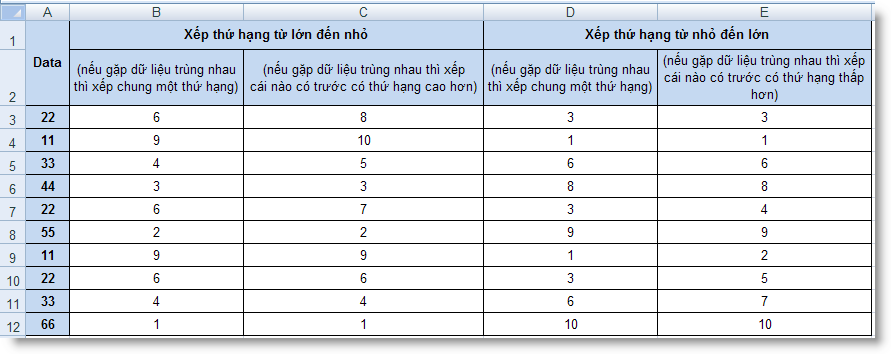
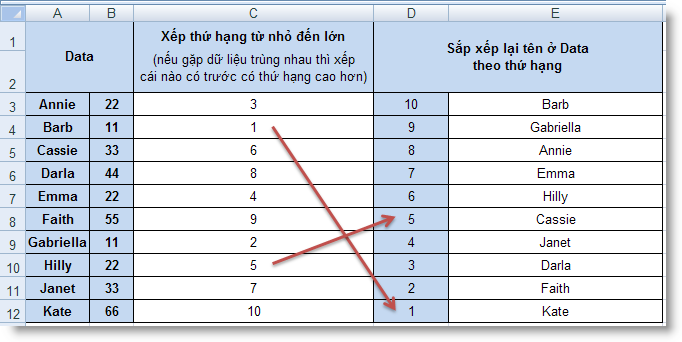
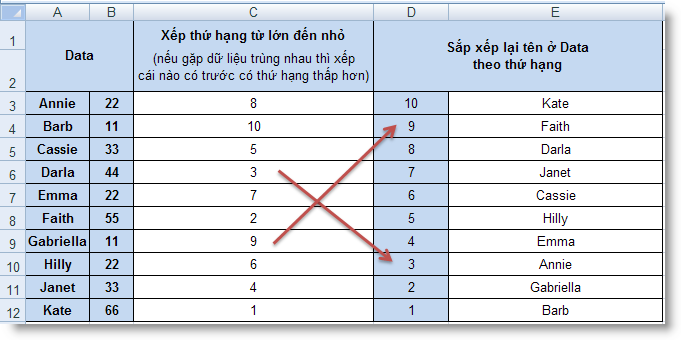
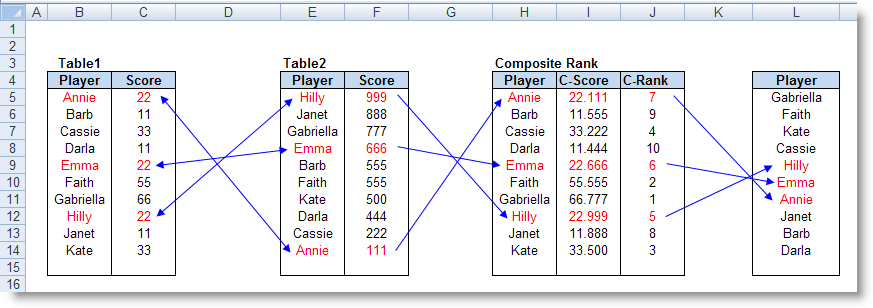
RANK (number, ref, order) : Tính thứ hạng của một số trong danh sách các số
SKEW (number1, number2, ...) : Trả về độ lệch của phân phối, mô tả độ không đối xứng của phân phối quanh trị trung bình của nó
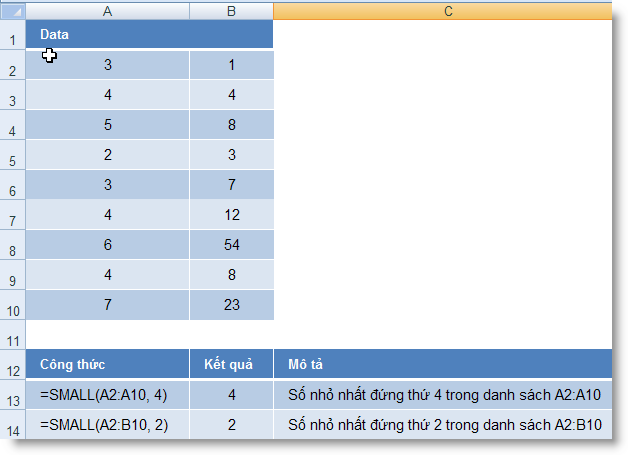
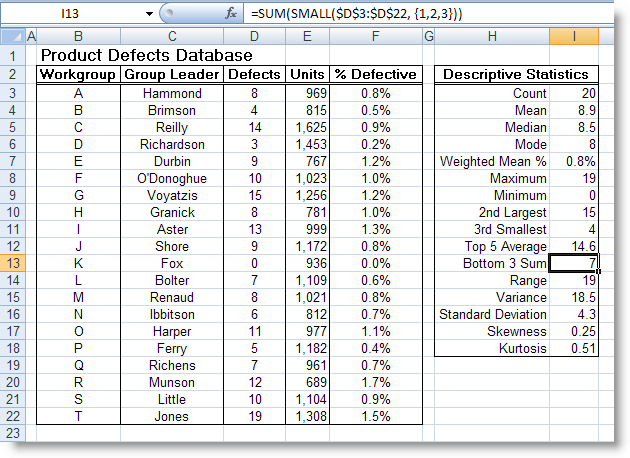
SMALL (array, k) : Trả về giá trị nhỏ nhất thứ k trong một tập số
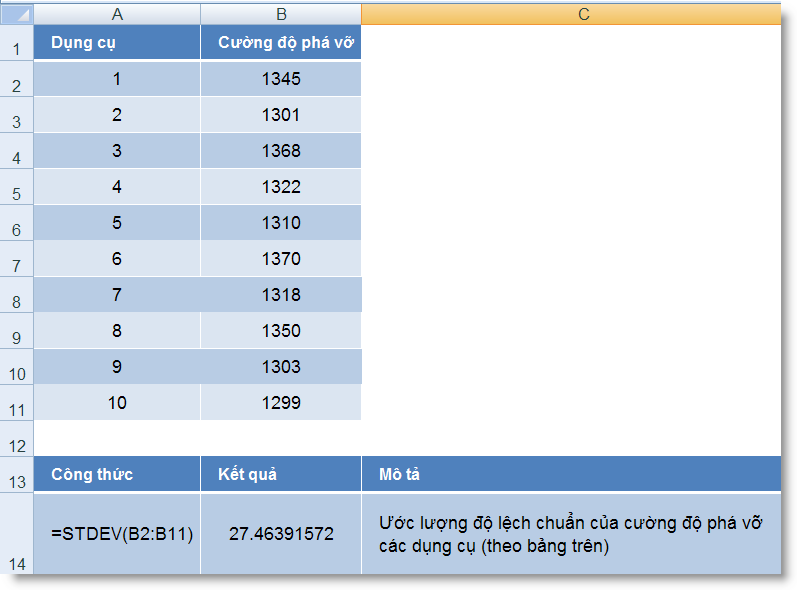
STDEV (number1, number2, ...) : Ước lượng độ lệch chuẩn trên cơ sở mẫu
STDEVA (value1, value2, ...) : Ước lượng độ lệch chuẩn trên cơ sở mẫu, bao gồm cả những giá trị logic
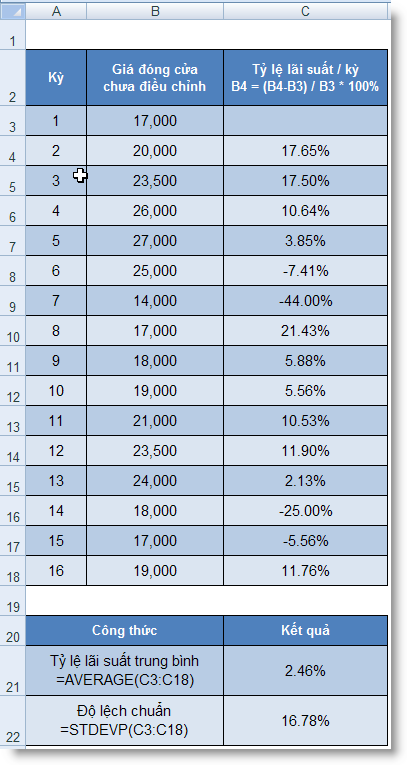
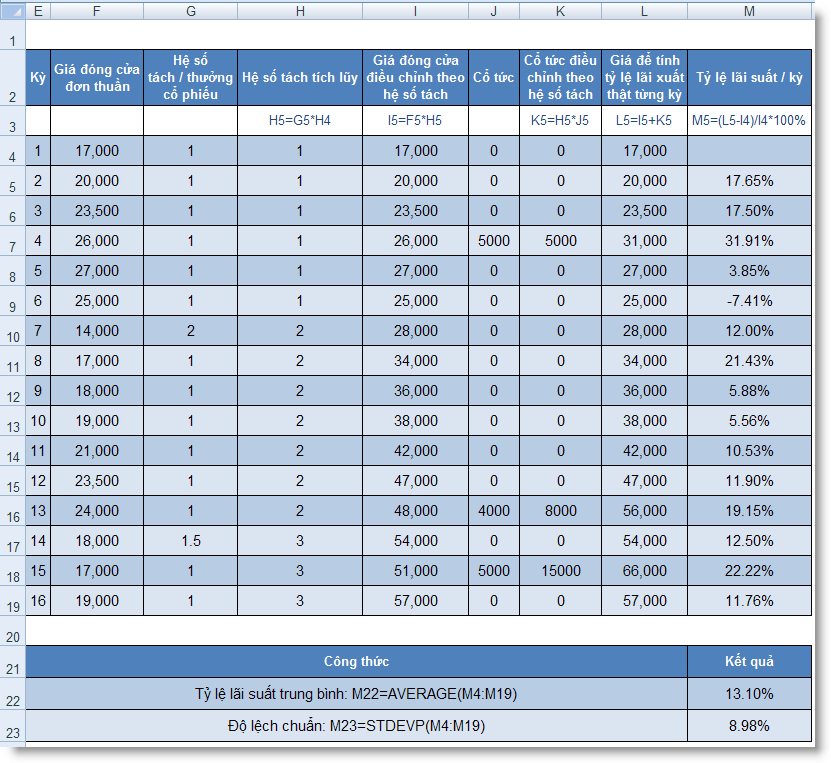
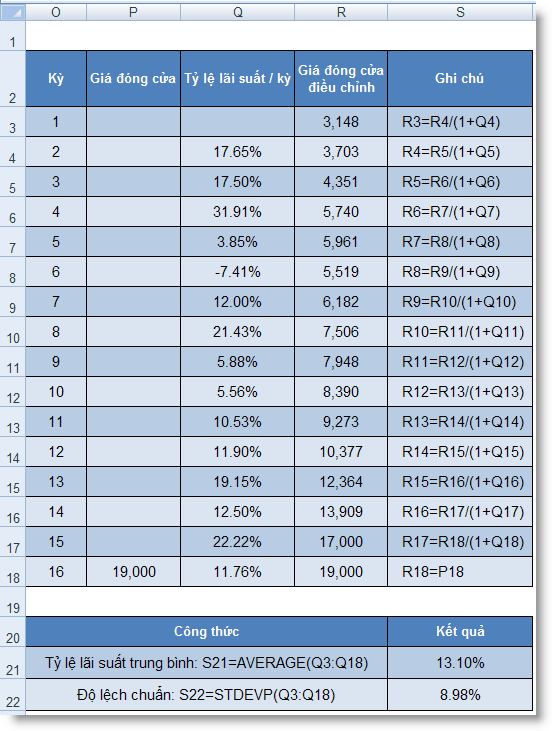
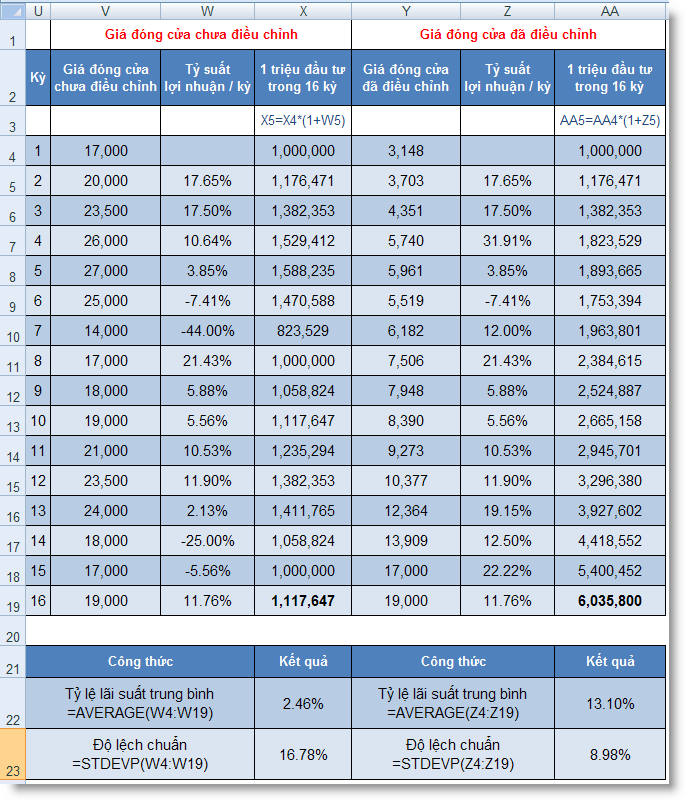
STDEVP (number1, number2, ...) : Tính độ lệch chuẩn theo toàn thể tập hợp
STDEVPA (value1, value2, ...) : Tính độ lệch chuẩn theo toàn thể tập hợp, kể cả chữ và các giá trị logic
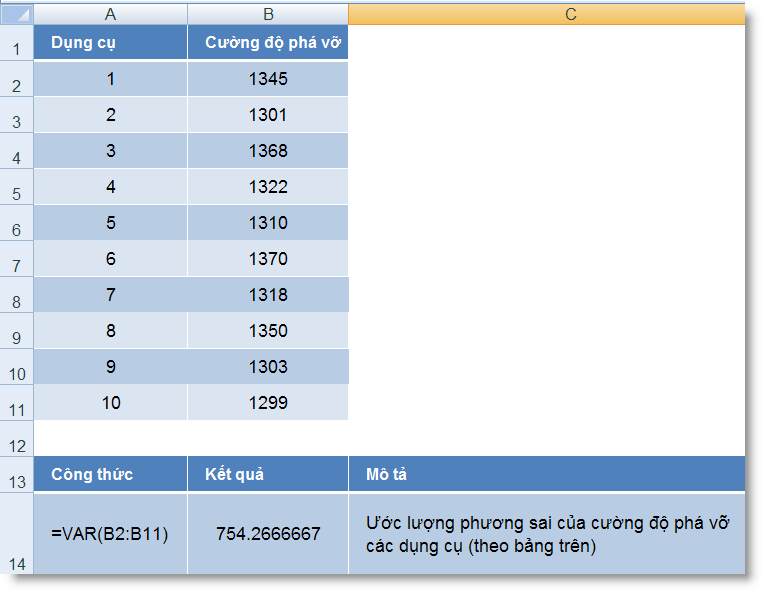
VAR (number1, number2, ...) : Trả về phương sai dựa trên mẫu
VARA (value1, value2, …) : Trả về phương sai dựa trên mẫu, bao gồm cả các trị logic và text
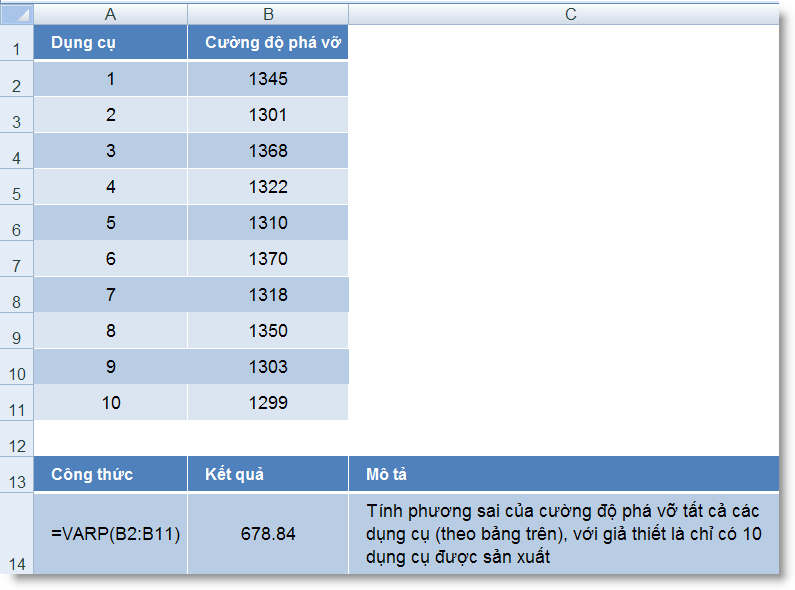
VARP (number1, number2, ...) : Trả về phương sai dựa trên toàn thể tập hợp
VARPA (value1, value2, …) : Trả về phương sai dựa trên toàn thể tập hợp, bao gồm cả các trị logic và text.
TRIMMEAN (array, percent) : Tính trung bình phần trong của một tập dữ liệu, bằng cách loại tỷ lệ phần trăm của các điểm dữ liệu ở đầu và ở cuối tập dữ liệu.
AVERAGE (number1, number2, ...) : Tính trung bình cộng
AVERAGEA (number1, number2, ...) : Tính trung bình cộng của các giá trị, bao gồm cả những giá trị logic
AVERAGEIF (range, criteria1) : Tính trung bình cộng của các giá trị trong một mảng theo một điều kiện
AVERAGEIFS (range, criteria1, criteria2, ...) : Tính trung bình cộng của các giá trị trong một mảng theo nhiều điều kiện
COUNT (value1, value2, ...) : Đếm số ô trong danh sách
COUNTA (value1, value2, ...) : Đếm số ô có chứa giá trị (không rỗng) trong danh sách
COUNTBLANK (range) : Đếm các ô rỗng trong một vùng
COUNTIF (range, criteria) : Đếm số ô thỏa một điều kiện cho trước bên trong một dãy
COUNTIFS (range1, criteria1, range2, criteria2, …) : Đếm số ô thỏa nhiều điều kiện cho trước
DEVSQ (number1, number2, ...) : Tính bình phương độ lệch các điểm dữ liệu từ trung bình mẫu của chúng, rồi cộng các bình phương đó lại.
FREQUENCY (data_array, bins_array) : Tính xem có bao nhiêu giá trị thường xuyên xuất hiện bên trong một dãy giá trị, rồi trả về một mảng đứng các số. Luôn sử dụng hàm này ở dạng công thức mảng
GEOMEAN (number1, number2, ...) : Trả về trung bình nhân của một dãy các số dương. Thường dùng để tính mức tăng trưởng trung bình, trong đó lãi kép có các lãi biến đổi được cho trước…
HARMEAN (number1, number2, ...) : Trả về trung bình điều hòa (nghịch đảo của trung bình cộng) của các số
KURT (number1, number2, ...) : Tính độ nhọn của tập số liệu, biểu thị mức nhọn hay mức phẳng tương đối của một phân bố so với phân bố chuẩn
LARGE (array, k) : Trả về giá trị lớn nhất thứ k trong một tập số liệu
MAX (number1, number2, ...) : Trả về giá trị lớn nhất của một tập giá trị
MAXA (number1, number2, ...) : Trả về giá trị lớn nhất của một tập giá trị, bao gồm cả các giá trị logic và text
MEDIAN (number1, number2, ...) : Tính trung bình vị của các số.
MIN (number1, number2, ...) : Trả về giá trị nhỏ nhất của một tập giá trị
MINA (number1, number2, ...) : Trả về giá trị nhỏ nhất của một tập giá trị, bao gồm cả các giá trị logic và text
MODE (number1, number2, ...) : Trả về giá trị xuất hiện nhiều nhất trong một mảng giá trị
PERCENTILE (array, k) : Tìm phân vị thứ k của các giá trị trong một mảng dữ liệu
PERCENTRANK (array, x, significance) : Trả về thứ hạng (vị trí tương đối) của một trị trong một mảng dữ liệu, là số phần trăm của mảng dữ liệu đó
PERMUT (number, number_chosen) : Trả về hoán vị của các đối tượng.
QUARTILE (array, quart) : Tính điểm tứ phân vị của tập dữ liệu. Thường được dùng trong khảo sát dữ liệu để chia các tập hợp thành nhiều nhóm…
RANK (number, ref, order) : Tính thứ hạng của một số trong danh sách các số
SKEW (number1, number2, ...) : Trả về độ lệch của phân phối, mô tả độ không đối xứng của phân phối quanh trị trung bình của nó
SMALL (array, k) : Trả về giá trị nhỏ nhất thứ k trong một tập số
STDEV (number1, number2, ...) : Ước lượng độ lệch chuẩn trên cơ sở mẫu
STDEVA (value1, value2, ...) : Ước lượng độ lệch chuẩn trên cơ sở mẫu, bao gồm cả những giá trị logic
STDEVP (number1, number2, ...) : Tính độ lệch chuẩn theo toàn thể tập hợp
STDEVPA (value1, value2, ...) : Tính độ lệch chuẩn theo toàn thể tập hợp, kể cả chữ và các giá trị logic
VAR (number1, number2, ...) : Trả về phương sai dựa trên mẫu
VARA (value1, value2, …) : Trả về phương sai dựa trên mẫu, bao gồm cả các trị logic và text
VARP (number1, number2, ...) : Trả về phương sai dựa trên toàn thể tập hợp
VARPA (value1, value2, …) : Trả về phương sai dựa trên toàn thể tập hợp, bao gồm cả các trị logic và text.
TRIMMEAN (array, percent) : Tính trung bình phần trong của một tập dữ liệu, bằng cách loại tỷ lệ phần trăm của các điểm dữ liệu ở đầu và ở cuối tập dữ liệu.
-------------------------------------------
2. Nhóm hàm về Phân Phối Xác Suất ...
3. Nhóm hàm về Tương Quan và Hồi Quy Tuyến Tính ...