Bài tập theo sách "Excel ứng dụng - Phân tích HĐKD và TCKT

[handung107]

Đây là các bài tập và bài giải có trong sách " Excel ứng dụng phân tích HĐKD và Tài chính kế tóan" của Đinh Thế hiển. Thú thực, về tài chính, tôi không rành lắm, nên bạn nào có khả năng tiếp sức giùm...

CHƯƠNG 1 - CÁC HÀM THỐNG KÊ VÀ TÀI CHÍNH

Thí dụ 1 : Cty Tài Chính DIFC đang phân tích biến động cổ phiếu của ngành sản xuất ô tô. Cty đang thu thập các dữ liệu về cổ phiếu của các Cty SX ô tô trong 3 năm chứa trong các Sheet Excel như sau :

- Giá cổ phiếu các năm của các công ty sản xuất ô tô (ĐVT : ngàn đồng)

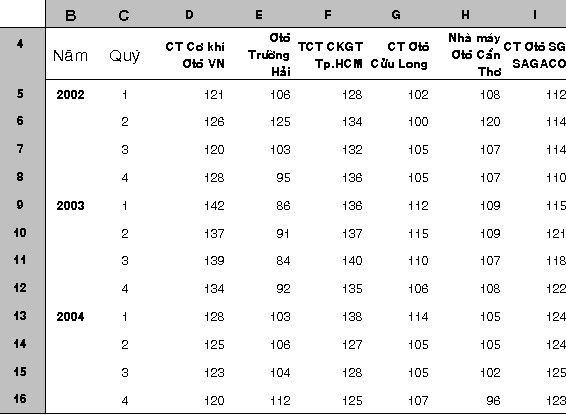
Hãy tính phương sai và độ lệch chuẩn của từng công ty và của toàn ngành sản xuất ô tô

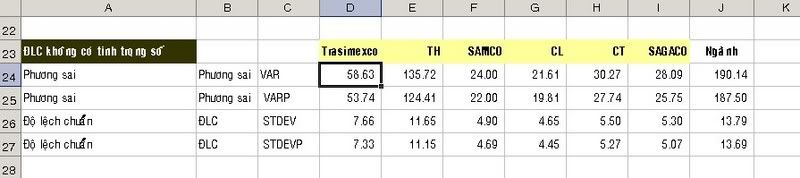
Để tính phương sai của từng công ty, tại Cell D24 ta lập công thức sau : =VAR(D516), trong đó khối (D516) chứa dữ liệu của công ty Trasimexco, sau đó ta AutoFill kéo ngang đến Cell I24, kết quả phương sai của từng công ty sẽ hiện ra như trên

Để tính phương sai của ngành SX ô tô, tại Cell J24 ta lập công thức sau : =VAR(D5:I16), trong đó khối D5:I16 chứa dữ liệu của các công ty

Thực hiện tương tự cho các hàm tiếp theo VARP, STDEV, STDEVP. Ta nhận thấy kết quả của hàm VAR và VARP có khác nhau một ít, tương tự hàm STDEV và STDEVP cũng vậy. Như vậy, tùy theo dữ liệu thu thập là một phần của tập hợp hay toàn bộ tập hợp mà chúng ta sử dụng hàm cho thích hợp

Khi lấy căn bậc hai của phương sai, chúng ta sẽ được độ lệch chuẩn

- Phương sai và độ lệch chuẩn thường dùng để tính các hệ số trong phân tích chứng khoán và phân tích rủi ro. Để hiểu rõ hơn phương sai và độ lệch chuẩn, chúng ta có thể tham khảo các sách về nguyên lý thống kê

 

[Don_Oliver]

Bạn có thể giải thích sự khác nhau giữa VAR và VARP cũng như STDEV và
STDEVP ko ? Cám ơn bạn.

 

[Nguyễn Duy Tuân]

VAR : là phương sai mẫu. Phương sai mẫu là chỉ tiêu tính ra độ biến thiên (hay gọi là bình phương độ phân tán) của các giá trị xung quanh giá trị trung tâm (giá trị trung bình cộng) của nó.
Ví dụ: có 2 tổ công nhân, T1 và T2
Số sản phẩm trung bình mỗi người T1=20 chiếc, T2=20 chiếc
Nếu đánh giá năng suất lao động của T1=T2 thì chưa chính xác. Để chính xác người ta cần tính ra độ phân tán.
Nếu VAR của T1=4, T2=10. Khi đó người ta có thể đánh giá trình độ lao động của T1 là tốt hơn T2 vì T1 số sản phẩm phân tán mỗi người thấp hơn T2.
Một ví dụ khác là đánh giá thu nhập người dân của một quốc gia, nếu người ta chỉ dựa vào thu nhập bình quân mỗi người để đánh giá là nước đó có thu nhập tốt hay không là không đúng, (ít nhất là về chỉ tiêu lượng).
VARA : tương tự như VAR, khác nhau ở VAR thì không tính các giá trị Logic, Text. Còn VARA tính tính tất cả.

VARP : Tương tự như VAR nhưng nó được tính trên số số đông.
Khi nghiên cứu hiện tượng kinh tế xã hội người ta đưa ra 2 khái niệm:
- Suy luận mẫu (sample) - Chọn mẫu
- Suy luận tổng thể (population)
Các công ty, đơn vị thường phải làm theophuwowng pháp chọn mẫu: thya vì phải nghiên cứu nhu cầu thị trường của 80 triệu dân người ta chỉ cần nghiên cứu 100 thôi
n (sample)= 80
N (population)=80 000 000
n càng lớn thì độ tin cậy càng cao!

STDEV: là độ lệch chuẩn. Nó là căn bậc hai của Phương sai (VAR)
Vì VAR tính ra giá trị độ lệch bình phương, nên số liệu thường không thật. Người ta hay dùng STDEV thay cho VAR.

STDEVP : giải thích như với VARP

chứ P= Population.

 

[PhanTuHuong]

Muốn hiểu hơn các hàm thống kê, bạn nên đọc sách về Xác suất thống kê. Cái này rất hợp với dân kỹ thuật.