You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Phương pháp tính hệ số cho phương trình bậc hai cho người học excel cơ bản (1 người xem)
- Thread starter nguyễn thanh tùng3288
- Ngày gửi
Người dùng đang xem chủ đề này
Đang trực tuyến: 1 (Thành viên: 0, Khách: 1)
Với 2 dạng dưới công thức sẽ như thế nào bạn ?
a*x^b+c
a*e^bx +c
Nói thực lòng là tôi không biết. Cách dùng trong bài 21 tôi đọc tài liệu của Microsoft và chỉ có vậy.Với 2 dạng dưới công thức sẽ như thế nào bạn ?
a*x^b+c
a*e^bx +c
Kể cả 2 tham số (3 và 4) của hàm Linest tôi cũng chưa thử dùng vì chưa hiểu ý nghĩa của nó. Vời mức độ sử dụng ở bài 21, tôi đã đối chiếu so khớp với equation của trend line của biểu đồ
Lần chỉnh sửa cuối:
Hồi quy phi tuyến dùng phương pháp đổi biến số trở thành hồi quy tuyến tính nhằm đơn giản cách tính các tham số, nhưng có nhược điểm là độ tin cậy không cao so với cách điều tiết trực tiếp từ đường hồi quy gốc. Trong file minh họa 1 ví vụ về sai số của hàm Linest khá lớn so với cách dùng công cụ Solver
File đính kèm
nguyễn thanh tùng3288
Thành viên mới

- Tham gia
- 2/6/21
- Bài viết
- 17
- Được thích
- 0
Cám ơn các bạn đã giúp đỡ tôi trong bài viết này, tôi không phải là người giỏi về excel nên không hiểu nhiều những cái các bạn nói, chỗ ptm0412 đã chỉ ra tôi nhầm trục tọa độ, nay tôi xin up lại file lần nữa ở hai dạng trục tọa độ và xin nhờ các bạn chỉnh trực tiếp trên file vì tôi đã tự làm tối qua đến nay vẫn không ra kết quả! xin chân thành cảm ơn!
File đính kèm
Khi dùng

Copy xuống O10 và O11
(Hai sheet công thức y hệt nhau, tuy nhiên sheet có hình 2 truy xuất đúng giá trị khi X = 6, Y = 1.35, sheet 1 phải truy xuất ngược Y = 6 ra X và phải giải phương trình)
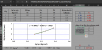
Khi dùng Linest (vẽ trend line trên đồ thị), cần phân tích dữ liệu, chọn loại hồi quy, thử và chọn lại mới tìm được dạng hồi quy gần đúng nhất. Ví dụ 2 biểu đồ trong file của anh, chọn hồi quy đa thức bậc 2 sẽ gần đúng nhất, bình phương độ chặt (R- squared) gần bằng 1).Hồi quy phi tuyến dùng phương pháp đổi biến số trở thành hồi quy tuyến tính nhằm đơn giản cách tính các tham số, nhưng có nhược điểm là độ tin cậy không cao so với cách điều tiết trực tiếp từ đường hồi quy gốc. Trong file minh họa 1 ví vụ về sai số của hàm Linest khá lớn so với cách dùng công cụ Solver

Bài đã được tự động gộp:
O9 =INDEX(LINEST($P$4:$P$6,$O$4:$O$6^{1,2}),ROW(A1))chỗ ptm0412 đã chỉ ra tôi nhầm trục tọa độ, nay tôi xin up lại file lần nữa ở hai dạng trục tọa độ
Copy xuống O10 và O11
(Hai sheet công thức y hệt nhau, tuy nhiên sheet có hình 2 truy xuất đúng giá trị khi X = 6, Y = 1.35, sheet 1 phải truy xuất ngược Y = 6 ra X và phải giải phương trình)


Lần chỉnh sửa cuối:
Mình chỉ đưa ví dụ hạn chế của hàm Linest khi tính các tham số của hồi quy phi tuyến, chưa xét dạng nào phù hợp nhất vì dữ liệu chỉ có 3 dòng, đường bậc 2 chắc chắn có R=1Khi dùng
Khi dùng Linest (vẽ trend line trên đồ thị), cần phân tích dữ liệu, chọn loại hồi quy, thử và chọn lại mới tìm được dạng hồi quy gần đúng nhất. Ví dụ 2 biểu đồ trong file của anh, chọn hồi quy đa thức bậc 2 sẽ gần đúng nhất, bình phương độ chặt (R- squared) gần bằng 1).
View attachment 260031
Bài đã được tự động gộp:
O9 =INDEX(LINEST($P$4:$P$6,$O$4:$O$6^{1,2}),ROW(A1))
Copy xuống O10 và O11
(Hai sheet công thức y hệt nhau, tuy nhiên sheet có hình 2 truy xuất đúng giá trị khi X = 6, Y = 1.35, sheet 1 phải truy xuất ngược Y = 6 ra X và phải giải phương trình)
View attachment 260034
View attachment 260035
Tôi xem kỹ thì đúng là trường hợp chỉ có 3 dòng, Linest có sai số lớn hơn solverMình chỉ đưa ví dụ hạn chế của hàm Linest khi tính các tham số của hồi quy phi tuyến, chưa xét dạng nào phù hợp nhất vì dữ liệu chỉ có 3 dòng, đường bậc 2 chắc chắn có R=1
Tuy nhiên biểu đồ anh vẽ có chỗ sai: giá trị point thứ 3 đang có giá trị (4, 49.93), giá trị đúng là (3, 49.93)

Sửa lại thì solver khép kín Y hơn là Linest

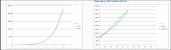
Ngoài ra tôi còn test thử trường hợp 6 dòng dữ liệu, và sự biến thiên của dữ liệu gần với hàm số mũ hơn, để khi Linest Power (hoặc chọn trend line của biểu đồ), phù hợp với dữ liệu hơn. Sau khi test thì dù cho tổng bình phương sai số 2 phương pháp khác nhau nhiều, nhưng cả 2 đều khép sát đường dữ liệu gốc, trừ point cuối.
File đính kèm
Kiểm tra lại, dùng Linest điều tiết đường hồi quy phải đổi biến Y bằng hàm log như a.x^b và a.e^bx có các tham số hồi quy không chính xác và độ tin cậy đường hồi quy không cao, các đường hồi quy còn lại đường hồi quy chính xácTôi xem kỹ thì đúng là trường hợp chỉ có 3 dòng, Linest có sai số lớn hơn solver
Tuy nhiên biểu đồ anh vẽ có chỗ sai: giá trị point thứ 3 đang có giá trị (4, 49.93), giá trị đúng là (3, 49.93)
View attachment 260063
Sửa lại thì solver khép kín Y hơn là Linest
View attachment 260064
Ngoài ra tôi còn test thử trường hợp 6 dòng dữ liệu, và sự biến thiên của dữ liệu gần với hàm số mũ hơn, để khi Linest Power (hoặc chọn trend line của biểu đồ), phù hợp với dữ liệu hơn. Sau khi test thì dù cho tổng bình phương sai số 2 phương pháp khác nhau nhiều, nhưng cả 2 đều khép sát đường dữ liệu gốc, trừ point cuối.
View attachment 260065
Nếu để so sánh Linest với solver thì: Linest tính toán bằng phương pháp tính bình phương bé nhất (hoặc phương pháp gì khác và có lẽ chỉ tính 1 lần), còn solver là cách tính lặp cho đến khi sai số nhỏ nhất, nên chắc chắn solver phải chính xác hơn LinestKiểm tra lại, dùng Linest điều tiết đường hồi quy phải đổi biến Y bằng hàm log như a.x^b và a.e^bx có các tham số hồi quy không chính xác và độ tin cậy đường hồi quy không cao, các đường hồi quy còn lại đường hồi quy chính xác
Hiện nay theo mình biết có 2 phương pháp điều tiết đường hồi quy là phương pháp bình phương bé nhất (bình phương sai số bé nhất) và phương pháp Newton, trong đó phương pháp bình phương bé nhất dể hơn và được sử dụng phổ biến, nó lập hệ phương trình chuẩn tắc tìm tham số hồi quy qua việc tìm cực trị bằng cách cho đạo hàm bậc 1 của từng tham số = 0Nếu để so sánh Linest với solver thì: Linest tính toán bằng phương pháp tính bình phương bé nhất (hoặc phương pháp gì khác và có lẽ chỉ tính 1 lần), còn solver là cách tính lặp cho đến khi sai số nhỏ nhất, nên chắc chắn solver phải chính xác hơn Linest
Hàm Linest và Solve mình lập đều dựa trên bình phương sai số bé nhất, Linest giải trực tiếp dựa trên hệ phương trình chuẩn tắc nên chính xác tuyệt đối với điều kiện không đổi biến Y để lập hệ phương trình chuẩn tắc, Solver là phương pháp tìm gần đúng nên có sai số cho phép nhất định
Phương pháp bình phương sai số bé nhất có nhược điểm là bình phương sai số sẽ khuếch đại sai số, để tìm chính xác sai số phải dựa vào tổng chênh lệch tuyệt đối biến Y của đường hồi quy và giá trị thực, cách nầy không tìm được hệ phương trình chuẩn tắc nên không được áp dụng
Bài viết mới nhất
- Trả lời
- 5
- Đọc
- 143
- Trả lời
- 2
- Đọc
- 63
- Trả lời
- 15
- Đọc
- 637
- Trả lời
- 2
- Đọc
- 69
- Trả lời
- 2
- Đọc
- 120
- Trả lời
- 1
- Đọc
- 114
- Trả lời
- 4
- Đọc
- 95
- Trả lời
- 670
- Đọc
- 265K
Phiên bản mới Add-in A-Tools v10 (2024)
(1 người xem)
- Trả lời
- 43
- Đọc
- 3K
- Trả lời
- 6
- Đọc
- 163
- Trả lời
- 5
- Đọc
- 93
- Trả lời
- 4
- Đọc
- 83
- Trả lời
- 4
- Đọc
- 177
- Trả lời
- 2
- Đọc
- 123
- Trả lời
- 12
- Đọc
- 233
- Question
- Trả lời
- 1
- Đọc
- 268
- Trả lời
- 5
- Đọc
- 131
- Question
- Trả lời
- 35
- Đọc
- 5K
- Trả lời
- 3
- Đọc
- 145
- Trả lời
- 12
- Đọc
- 17K
Thành viên có số lượng bài viết cao nhất tháng
- ptm0412 29
- VetMini 23
- HeSanbi 16
- BuiQuangThuan 11
- befaint 10
- A HOANG 620 9
- Hoàng Tuấn 868 9
- bebo021999 9
- HUONGHCKT 9
- SA_DQ 7
- DeTong 7
- thuong-minh 6
- minhminh27 6
- tt_kimbai 6
- Em khong biet 6
- Hoale85 5
- thuytrangbp28 5
- Cuong_98 5
- hailuatv 5
- hoangluongvinh 5
Thành viên có điểm tương tác cao nhất tháng
- VetMini 20
- ptm0412 19
- HeSanbi 17
- SA_DQ 11
- HUONGHCKT 10
- BuiQuangThuan 9
- Hoàng Tuấn 868 7
- GPE-Trợ Lý 7
- hoangtuan.net 6
- yaaasoo01 4
- hoangtuaotrang_hp_vn 4
- tranhungdao12a3 3
- befaint 3
- DeTong 3
- bebo021999 3
- Duy Tùng 9x 2
- vietduc147258 2
- Phuocam 1
- Em khong biet 1
- ongke0711 1




