Xin chào mọi người.
Em có 1 bài toán.
Sau khi thu thập số liệu từ máy toàn đạc, yêu cầu là tìm ra bán kính và toạ độ tâm hình cầu.
Cách làm như sau:
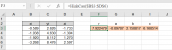
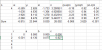
Giả sử có 4 điểm (thực tế khoảng 40 hoặc nhiều hơn) như trong hình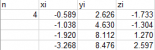
Ban đầu ta giả thuyết rằng tâm hình cầu có toạ độ là (a1,b1,c1) = (0,0,0) bán kính r1=0
B1: Ta sẽ tính được khoảng cách từ tâm đến các điểm theo công thức = sqrt{ (0-xi)^2 + (0-yi)^2 + (0-zi)^2 }
B2: Tính tổng các giá trị trên chia cho số điểm ta được bán kính mới là r2
B3: Tính các giá trị (xi-a)/ri, (yi-b)/ri, (zi-b)/ri
Tổng từng giá trị trên
B4: Tìm được tâm mới theo công thức a2 = sum(xi)-r2*sum((xi-a)/ri))/n, tương tự cho b2, c2
Sau khi có r2, và tâm mới (a2, b2. c2) lặp lại B1-B4 để có r3 và tâm mới (a3, b3, c3)
Lặp lại quá trình trên cho đến khi nào độ lệch của ri và ri+1 là 0.00001
Nhờ mọi người viết giúp em công thức vòng lặp để tính cho nhanh.
Em cảm ơn.
Em có 1 bài toán.
Sau khi thu thập số liệu từ máy toàn đạc, yêu cầu là tìm ra bán kính và toạ độ tâm hình cầu.
Cách làm như sau:
Giả sử có 4 điểm (thực tế khoảng 40 hoặc nhiều hơn) như trong hình

Ban đầu ta giả thuyết rằng tâm hình cầu có toạ độ là (a1,b1,c1) = (0,0,0) bán kính r1=0
B1: Ta sẽ tính được khoảng cách từ tâm đến các điểm theo công thức = sqrt{ (0-xi)^2 + (0-yi)^2 + (0-zi)^2 }
B2: Tính tổng các giá trị trên chia cho số điểm ta được bán kính mới là r2
B3: Tính các giá trị (xi-a)/ri, (yi-b)/ri, (zi-b)/ri
Tổng từng giá trị trên
B4: Tìm được tâm mới theo công thức a2 = sum(xi)-r2*sum((xi-a)/ri))/n, tương tự cho b2, c2

Sau khi có r2, và tâm mới (a2, b2. c2) lặp lại B1-B4 để có r3 và tâm mới (a3, b3, c3)
Lặp lại quá trình trên cho đến khi nào độ lệch của ri và ri+1 là 0.00001
Nhờ mọi người viết giúp em công thức vòng lặp để tính cho nhanh.
Em cảm ơn.