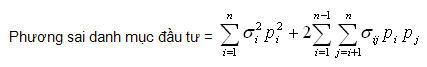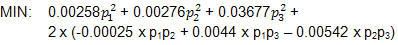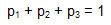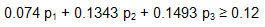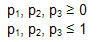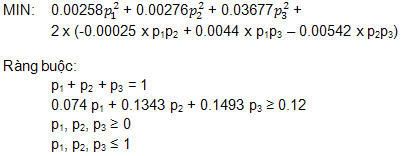Lựa chọn danh mục đầu tư

[TranThanhPhong]

Lựa chọn danh mục đầu tư (Portfolio)

Lựa chọn danh mục vốn đầu tư​

​

Một trong các ứng dụng nổi tiếng nhất của mô hình NLP là xác định các khoản đầu trong danh mục vốn đầu tư để giảm rủi ro đến mức thấp nhất và thu được lợi nhuận như mong muốn. Đối với việc đầu tư đơn lẻ thì thước đo mức rủi ro chính là sự biến thiên (phương sai) hoặc độ lệch chuẩn của lợi nhuận trong một số thời đoạn. Do vậy, mục tiêu chính của việc chọn lựa danh mục đầu tư là làm giảm đi (làm trơn) sự biến thiên của lợi nhuận thu về từ danh mục đầu tư bằng cách chọn đầu tư sao cho tổng lợi nhuận thu về có khuynh hướng biến đổi ngược chiều nhau. Vì thế chúng ta nên chọn các khoản đầu tư sao cho chúng có phương sai âm hoặc tương quan nghịch để khi mà một khoản đầu tư thu về lợi nhuận thấp hơn mức lợi nhuận trung bình thì sẽ có một khoản đầu tư khác thu về lợi nhuận cao hơn mức trung bình. Việc này làm cho sự biến thiên lợi nhuận của tập đầu tư nhỏ hơn sự biến thiên của việc đầu tư đơn lẻ.

a.Giới thiệu bài toán

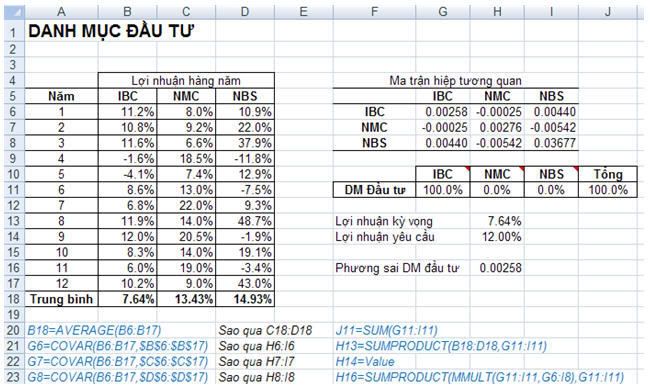
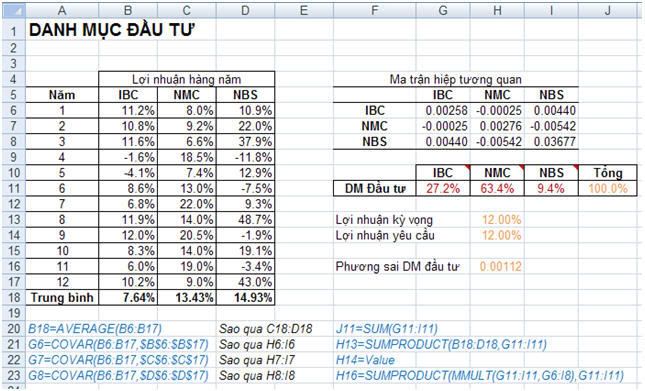
Mr.Okebab là nhà tư vấn tài chính độc lập. Ông ta gặp một khách hàng mới tên là Ms.SG, cô này muốn Mr.Okebab tư vấn để đa dạng hóa tập đầu tư của mình. Ms.SG đã đầu tư một phần vốn vào cổ phiếu IBC. Trong 12 năm qua cổ phiếu này có tỉ suất lợi nhuận hàng năm trung bình là 7.64% với phương sai xấp xĩ 0.0026. Ms.SG muốn có được nhiều lợi nhuận hơn từ các khoản đầu tư nhưng không muốn bị nhiều rủi ro. Ms.SG nhờ Mr.Okebab tư vấn cho một tập đầu tư sao cho thu về ít nhất lợi nhuận trung bình là 12% với rủi ro là thấp nhất. Sau khi nghiên cứu, Mr.Okebab xác định được thêm hai loại cổ phiếu mã là NMC và NBS có thể giúp Ms.SG thu được lợi nhuận mong muốn. Kết quả nghiên cứu tóm tắt như hình dưới đây.

​

Số liệu của tập đầu tư​

​

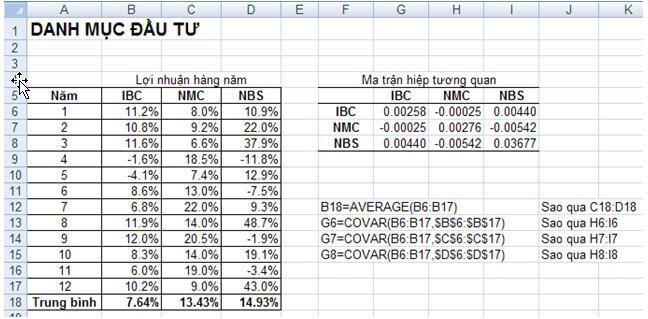
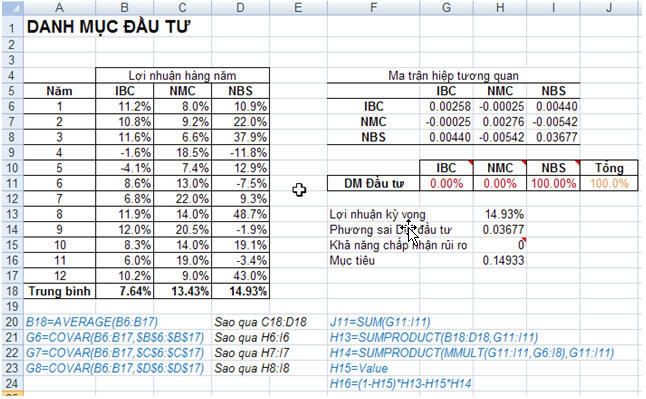
Theo kết quả nghiên cứu, ta thấy rằng cổ phiếu NMC có tỉ suất lợi nhuận trung bình là 13.43% trong 12 năm và cổ phiếu NBS đạt 14.93%. Mr.Okebab dùng hàm Covar() trong Excel để tạo nên ma trận hiệp tương quan (xem hình). Từ ma trận thấy rằng phương sai của tỷ suất lợi nhuận hàng năm của IBC, NMC và NBS lần lượt là 0.00258, 0.00276 và 0.03677. Các phần còn lại trong ma trận cho biết hiệp tương quan giữa các cặp chứng khoán, ví dụ như hiệp tương quan giữa IBC và NMC xấp xĩ 0.00440, giữa NMC và NBS xấp xĩ -0.00542.

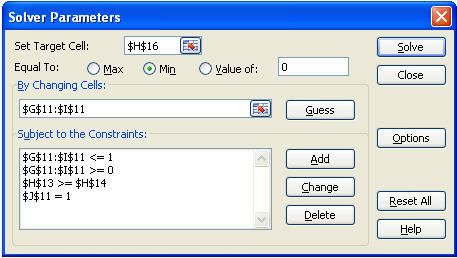
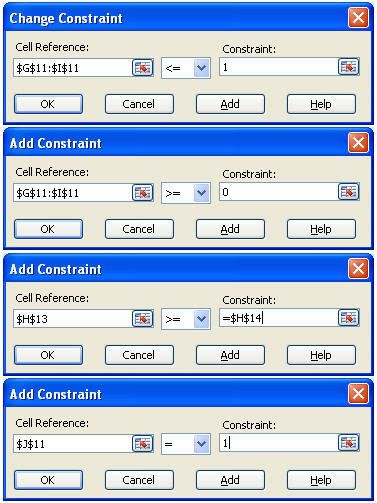
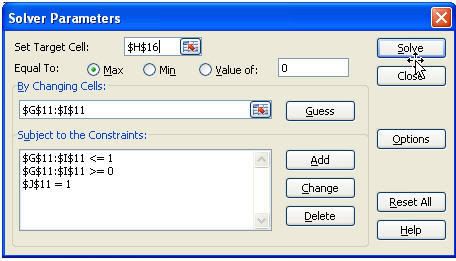
Mr.Okebab muốn xác định tỷ lệ đầu tư vào từng loại cổ phiếu nhằm đạt được tỷ lệ lợi nhuận mong muốn là 12% với điều kiện sự biến thiên (phương sai) của tổng lợi nhuận trong tập đầu tư là thấp nhất (rủi ro thấp nhất).

(còn tiếp)

TP.

 

[TranThanhPhong]

Xác định biến và hàm mục tiêu

Xác định các biến quyết định

Trong bài toán này chúng ta phải xác định tỷ lệ đầu từ vào từng loại cổ phiếu. Vì vậy, để giải quyết bài toán chúng ta cần có ba biến quyết định:

p1 = tỷ lệ trong tổng tiền đầu tư vào IBC
p2 = tỷ lệ trong tổng tiền đầu tư vào NMC
p3 = tỷ lệ trong tổng tiền đầu tư vào NBS

Bởi vì các biến này tượng trưng cho các tỷ lệ, do vậy chúng phải lớn hơn 0 và tổng của chúng phải bằng 1 (100%). Lưu ý phải đưa các điều kiện này vào khi giải bài toán.

Xác định mục tiêu

Mục tiêu trong bài toán này là tối thiểu hóa rủi ro của danh mục đầu tư dựa vào các trị thống kê phương sai. Một cách tổng quát, phương sai của danh mục đầu tư với n hạn mục đầu tư được xác định bởi công thức sau:

Trong đó:

Công thức trên tương đương với công thức ở dạng ma trận như sau:

Từ đó thế vào công thức trên ta được hàm mục tiêu như sau:

(còn tiếp)

TP.

 

[TranThanhPhong]

Các ràng buộc và lập mô hình lên bảng tính

Xác định các ràng buộc

Chỉ có hai ràng buộc chính cho bài toán này, theo đề bài chúng ta có 3 biến quyết định tượng trưng cho tỷ lệ của các hạn mục đầu tư trong danh mục đầu tư và tổng các tỷ lệ là 100%.

Ngoài ra chúng ta cũng cần thêm ràng buộc để tỷ lệ lợi nhuận mong muốn (kỳ vọng) của danh mục đầu tư là 12%.

Các hệ số chính là tỷ suất lợi nhuận trung bình của từng loại cổ phiếu. Ràng buộc trên để đảm bảo rằng tỷ suất lợi nhuận trung bình của tập đầu tư tối thiểu là 12%

Do các biến quyến định là các tỷ lệ nên chúng phải là số dương và tối đa là 1.

Triển khai mô hình lên bảng tính

Tóm tại bài toán có các thông tin sau:

Trình bày các lên bảng tính như hình bên dưới

• Các ô G11, H11 và I11 chính là các tỷ lệ đầu tư p1, p2, p3, ta nhập cho chúng các giá trị khởi động bất kỳ ví dụ như nhập vào G11 là 100%, H11 là 0% và I11 là 0%.
• Nhập vào ô H16 công thức sau: =G6*G11^2+H7*H11^2+I8*I11^2+2*(H6*G11*H11+I6*G11*I11+H8*H11*I11)
• Để đỡ tốn công nhập công thức trên ta có thể sử dụng hàm Sumproduct (Tính tổng các tính) kết hợp hàm Mmult (nhân ma trận) như sau: =SUMPRODUCT(MMULT(G11:I11,G6:I8),G11:I11)
• Tương tự tính cho ô lợi nhuận mong muốn tại H13 bằng hàm Sumproduct như sau: =SUMPRODUCT(B1818,G11:I11)
• Nhập lợi nhuận yêu cầu tại ô H14 giá trị là 12%

Mô hình bài toán trên bảng tính

​

(còn tiếp)

​

TP.
​

 

[TranThanhPhong]

Khai báo thông số cho Solver

Add-Ins Solver:

Excel 2007: Chọn Office à Excels Options à Add-Ins à Go… à chọn Sover Add-in à OK
Excel cũ: Tools à Add-Ins à chọn Sover Add-in à OK

​

Hộp thoại Add-Ins

Khai báo:

B1. Chọn ô H16
B2. Vào Ribbon à Analysis à Solver. (Các phiên bản Excel cũ vào Tools à Solver)
B3. Tại Set Target Cell chọn ô H16 (hàm mục tiêu) và tại Equal To thì chọn Min
B4. Tại By Changing Cells chọn G11:I11 (tỷ lệ các hạn mục đầu tư cần tìm)
B5. Thêm các ràng buộc vào bằng cách nhấn nút Add, làm tuần tuần tự cho tất cả các ràng buộc. Khai báo xong trong hộp thoại Change Constraint nếu muốn thêm ràng buộc khác thì nhất nút Add còn kết thúc thì nhấn nút OK để trở về hộp thoại Solver. (Xem các hình bên dưới)
​

​

Khai báo các thông số và các ràng buộc

B6. Nhấn nút Solve để tìm lời giải

Kết quả chạy Solver

(còn tiếp)

TP.

 

[TranThanhPhong]

Một số nhận xét

Một số nhận xét

• Kết quả cho thấy phương án đầu tư tốt hơn so với việc đầu tư đơn lẻ chính là đầu tư 27.2% tiền vào IBC, đầu tư 63.4% vào NMC và 9.4% vào NBS. Ô H13 cho thấy rằng tập đầu tư này sẽ đạt được mức lợi nhuận mong muốn là 12% và ô H16 cho thấy sự biến thiên của tập đầu tư chỉ là 0.00112 thấp hơn nhiều so với biến thiên của từng cổ phiếu đơn lẻ.
• Lời giải cho thấy tập đầu tư này sẽ mang lại lợi nhuận mong muốn cho Ms.SG với rủi ro thấp hơn việc đầu tư của cô ta trước kia và việc đầu tư trước kia là không hiệu quả. Lý thuyết về danh mục đầu tư cho rằng đối với mỗi mức lợi nhuận đầu tư có thể có thì sẽ tồn tại một tập đầu tư cho rủi ro thấp nhất và nếu chúng ta chọn nhầm một tập đầu tư mà có rủi ro cao hơn thì xem như tập đầu tư đó không có hiệu quả. Ngược lại, đối với mỗi mức rủi ro đầu tư thì sẽ tồn tại một tập đầu tư cho lợi nhuận cao nhất và nếu chúng ta chọn nhầm một tập đầu tư cho lợi nhuận thấp hơn thì cũng xem như tập đầu tư đó không có hiệu quả.
• Do vậy, dù chúng ta cố gắng giảm thiểu rủi ro để đạt được mức lợi nhuận cho trước hoặc chúng ta tối đa hóa lợi nhuận với một mức rủi ro cho trước thì kết quả thu được vẫn có khả năng là tập đầu tư không hiệu quả. Theo ý này, lời giải từ bài ví dụ trên có khả năng đưa ra tập đầu tư không hiệu quả vì có khả năng tồn tại một tập đầu tư khác hiệu quả hơn (vì đây là bài toán NLP – không tuyến tính).
• Để giải quyết vấn đề trên, giải lại bài toán nhiều lần và tăng mức lợi nhuận kỳ vọng lên trong khi vẫn giữ nguyên mức rủi ro. (Đặt ô H14 thành một số khác cao hơn và tại Equal To nhập vào giá trị tìm được lần đầu tiên tại ô H16).
• Để tối ưu sự đánh đổi giữa rủi ro và lợi nhuận cho tập đầu tư, chúng ta nên vẽ biểu đồ như hình bên dưới (từ kết quả thu về của nhiều lần chạy Solver có sự thay đổi rủi ro và mức lợi nhuận). Biểu đồ sẽ minh họa cho chúng ta mức rủi ro thấp nhất cho một mức tỷ suất lợi nhuận thu về nào đó.

(còn tiếp)

TP.

 

[TranThanhPhong]

Giải quyết mâu thuẫn giữa lợi nhuận và rủi ro

Giải quyết mâu thuẫn giữa lợi nhuận và rủi ro

Chúng ta thấy rằng có sự mâu thuẫn trong các mục tiêu của bài toán lựa chọn danh mục đầu tư trên: giảm thiểu rủi ro (phương sai tập đầu tư) và tối đa hóa lợi nhuận. Các giải quyết mâu thuẫn trên là chúng ta cùng giải tiếp bài toán sau:

Trong đó, pi chính là tỷ lệ tiền đầu tư vào các hạn mục đầu tư và r là một hằng số giữa 0 và 1 tượng trưng cho khả năng chấp nhận rủi ro của nhà đầu tư. Khi r=1 (rủi ro thấp nhất) thì mục tiêu của bài toán lúc này là tập trung làm giảm tối thiểu phương sai của tập đầu tư.

Chúng ta thử giải lại bài toán khi r=1, khai báo lại các thông số trên bảng tính như hình sau:

Gọi hộp thoại Solver và tại Set Target Cell chọn ô H16 và cho tiến tới Max, By Change Cells vẫn là các ô G11:I11 và các ràng buộc như hình dưới, sau đó nhấn nút Solve để xem kết quả.

Từ kết quả trên, chúng ta thấy rằng khi nhà đầu tư ’không thích rủi ro” r=1 thì tỷ suất lợi nhuận thu về trong trường hợp này 11.46% khi đó nhà đầu tư sẽ đầu tư 35.96% vào IBC, 56.96% vào NMC và 7.08% vào NBS. Với tập đầu tư này thì phương sai sẽ là 0.00110 thấp hơn phương sai của tập đầu tư xét ở trên.

Tương tự, khi r=0 (rủi ro cao nhất) thì mục tiêu lúc này là cực đại lợi nhuận thu về của tập đầu tư. Chúng ta thử giải lại bài toán khi r=0, khai báo lại các thông số trên bảng tính như hình sau:

Sửa lại giá trị ô H15 thành số 0 và chạy lại Solver, kết quả cho thấy nhà đầu tư sẽ đầu tư 100% vốn vào cổ phiếu NBS vì khi đó thu được lợi nhuận lớn nhất.

Đối với trường hợp giá trị 0 < r < 1 thì Solver sẽ cố gắng tìm kiếm lời giải sao cho lợi nhuận thu về là lớn nhất có thể và phương sai của tập đầu tư là nhỏ nhất có thể được. Khi r càng tiến về 1 thì rủi ro càng giảm, điều này phù hợp cho những nhà đầu tư không thích rủi ro. Tóm lại, đây là bài toán đánh đổi giữa lợi nhuận thu về và rủi ro phải chịu của nhà đầu tư, nếu bạn là người thích an toàn thì hãy chọn r là một con số gần với số 1 và ngược lại bạn thích đầu tư mạo hiềm thì hãy cho r gần với số 0, sự lựa chọn và quyết định đúng đắn sẽ mang bạn đến thành công.

(Hết)

TP.

 

[TranThanhPhong]

Lý thuyết rủi ro và lợi nhuận

Thị trường chứng khoán có tính rủi ro bởi vì có sự phân tán các kết quả có thể xảy ra. Thước đo thông dụng đối với sự phân tán này là độ lệch chuẩn hay phương sai. Rủi ro của bất kỳ chứng khoán nào cũng có thể được phân chia thành hai phần. Một phần là rủi ro riêng biệt (unique risk) mà chỉ riêng chứng khoán đó mới có, và một phần là rủi ro thị trường (market risk) gắn với những biến thiên trên toàn thị trường. Các nhà đầu tư có thể loại bỏ được rủi ro chuyên biệt bằng cách nắm giữ một danh mục chứng khoán được đa dạng hóa tốt nhưng họ không thể loại bỏ được các rủi ro thị trường. Tất cả rủi ro của một danh mục chứng khoán được đa dạng hóa tốt là rủi ro thị trường.

Mức độ một chứng khoán góp phần vào rủi ro của một danh mục chứng khoán được đa dạng hóa tốt phụ thuộc vào độ nhạy của nó trước những thay đổi trên thị trường. Độ nhạy này thường được gọi là beta. Chứng khoán với beta bằng 1,0 có mức rủi ro thị trường trung bình - một danh mục chứng khoán được đa dạng hóa tốt của các chứng khoán như thế có cùng độ lệch chuẩn như chỉ số thị trường. Một chứng khoán với beta bằng 0,5 có mức rủi ro thấp hơn mức rủi ro thị trường trung bình - một danh mục được đa dạng hóa tốt của các chứng khoán đó có khuynh hướng biến thiên bằng một nửa mức biến thiên trên thị trường và có độ lệch chuẩn bằng một nửa độ lệch chuẩn của thị trường.

 

[TranThanhPhong]

Lý thuyết danh mục đầu tư

Các bạn xem nội dung trong file đính kèm.

TP.