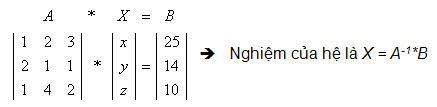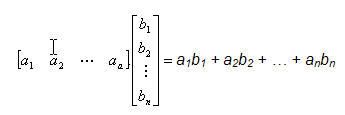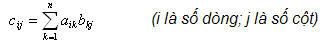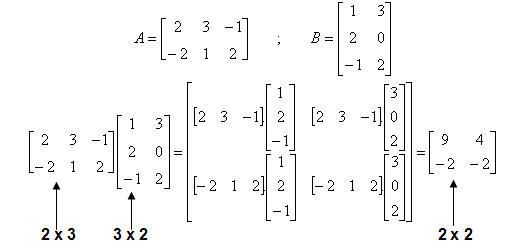- Tham gia
- 16/3/07
- Bài viết
- 2,104
- Được thích
- 19,177
- Giới tính
- Nam
Chào các bạn,
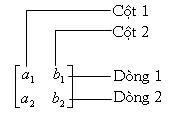
Mình xin giới thiệu với các bạn các giải hệ phương trình trong Excel bằng Solver và dùng các hàm ma trận.
Ví dụ: Giải hệ phương trình sau:
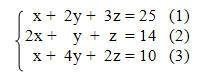
Cách 1. Giải hệ phương trình dùng Solver
B1. Xác định các biến, các hàm mục tiêu và lập mô hình trên bảng tính
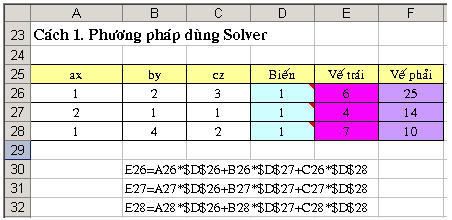
Lập mô hình bài toán trên bảng tính
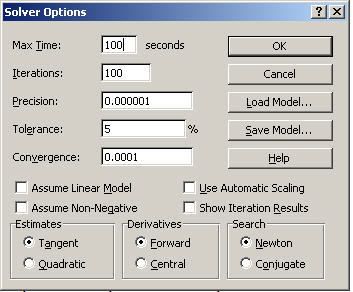
Ghi chú: Cách khác để tính nhanh Vế trái của các phương trình là dùng kết hợp hàm Sumproduct (array1, array2) và hàm Transpose (array). Cách làm như sau:
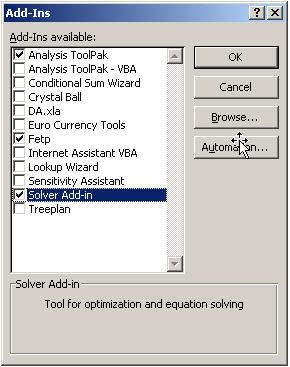
Hộp thoại Add-Ins chứa các chức năng mở rộng của Excel
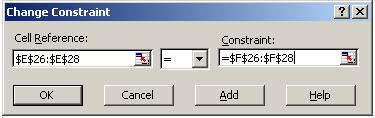
Thêm ràng buộc
Nhấp nút OK để hoàn tất.
Nếu bài toán cần nhiều ràng buộc hơn thì thực hiện lại hai bước trên để nhập thêm các ràng buộc khác.
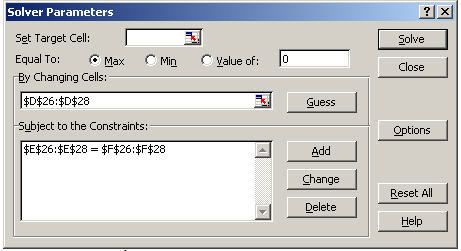
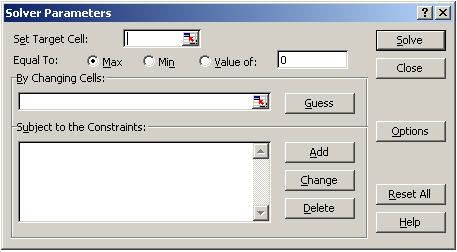
Khai báo thông số cho Solver
B3. Nhấp nút Solve chạy tìm lời giải. Hộp thông báo sau sẽ xuất hiện:
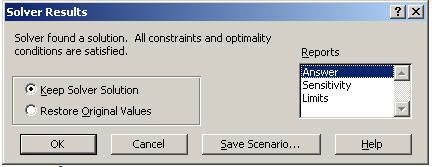
Chọn kiểu báo cáo
B4. Chọn Keep Solver Solution để lưu kết quả trên bảng tính. Chọn Restore Original Values để hủy kết quả Solver vừa tìm được và trả các biến về tình trạng ban đầu. Chọn Save Scenario để lưu kết quả vừa tìm được thành một tình huống để có xem lại sau này. Ngoài ra còn có 3 loại báo cáo là Answer, Sensitivity và Limits.
B5. Chọn OK để hoàn tất quá trình chạy Solver.

Các nghiệm hệ phương trình là: x=4, y=-3 và z=9
TP.
Mình xin giới thiệu với các bạn các giải hệ phương trình trong Excel bằng Solver và dùng các hàm ma trận.
Ví dụ: Giải hệ phương trình sau:
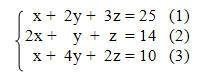
Cách 1. Giải hệ phương trình dùng Solver
B1. Xác định các biến, các hàm mục tiêu và lập mô hình trên bảng tính
- Các ô trong mảng A26:C28 nhập các hệ số của các phương trình (mỗi phương trình nhập một dòng).
- Các ô D26, D27, D28 lần lượt chứa giá trị khởi động của các biến x, y, z
- Các ô F26, F27, F28 lần lượt chứa các giá trị ở vế phải của các phương trình (1), (2) và (3).
- Các ô E26, E27, E28 được tính bằng cách nhân các hệ số của phương trình với các giá trị khởi động của x, y, z (xem công thức minh họa trong hình 5.6).

Lập mô hình bài toán trên bảng tính
Ghi chú: Cách khác để tính nhanh Vế trái của các phương trình là dùng kết hợp hàm Sumproduct (array1, array2) và hàm Transpose (array). Cách làm như sau:
- Chọn 3 ô E26 và nhập vào công thức sau:
=SUMPRODUCT(A26:C26,TRANSPOSE($D$26:$D$28))
- Sao chép công thức cho 2 ô còn lại E27 và E28.
- Vào thực đơn Tools à Add-Ins

Hộp thoại Add-Ins chứa các chức năng mở rộng của Excel
- Chọn Solver Add-in và chọn OK để chấp nhận.
- Đưa địa chỉ D26
 28 vào By Changing Cells
28 vào By Changing Cells - Đưa các ràng buộc vào Subject to the Constraints:

Thêm ràng buộc
Nhấp nút OK để hoàn tất.
Nếu bài toán cần nhiều ràng buộc hơn thì thực hiện lại hai bước trên để nhập thêm các ràng buộc khác.

Khai báo thông số cho Solver
B3. Nhấp nút Solve chạy tìm lời giải. Hộp thông báo sau sẽ xuất hiện:

Chọn kiểu báo cáo
B4. Chọn Keep Solver Solution để lưu kết quả trên bảng tính. Chọn Restore Original Values để hủy kết quả Solver vừa tìm được và trả các biến về tình trạng ban đầu. Chọn Save Scenario để lưu kết quả vừa tìm được thành một tình huống để có xem lại sau này. Ngoài ra còn có 3 loại báo cáo là Answer, Sensitivity và Limits.
B5. Chọn OK để hoàn tất quá trình chạy Solver.

Các nghiệm hệ phương trình là: x=4, y=-3 và z=9
TP.