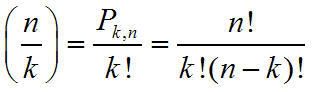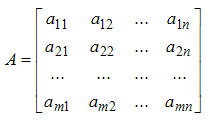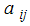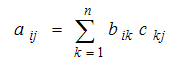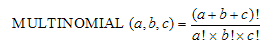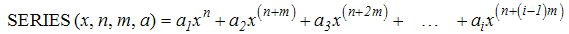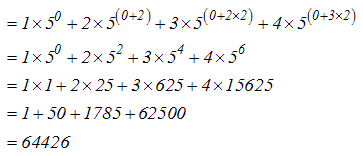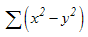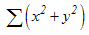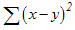- Tham gia
- 3/7/07
- Bài viết
- 4,946
- Được thích
- 23,213
- Nghề nghiệp
- Dạy đàn piano
List of Excel's Math Functions
Danh mục các hàm toán học
ABS (number): Tính trị tuyệt đối của một số (giá trị tuyệt đối của một số là số luôn luôn dương).
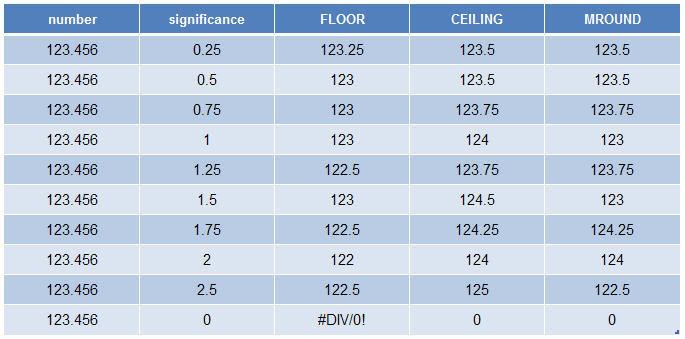
CEILING (number, significance) : Làm tròn lên một số (cách xa khỏi số 0) đến bội số gần nhất của significance.
COMBIN (number, number_chosen) : Trả về số tổ hợp được chọn từ một số các phần tử. Thường dùng để xác định tổng số nhóm có được từ một số các phần tử.
EVEN (number) : Làm tròn một số đến số nguyên chẵn gần nhất
EXP (number) : Tính lũy thừa cơ số e của một số
FACT (number) : Tính giai thừa của một số
FACTDOUBLE (number) : Tính giai thừa cấp hai của một số
FLOOR (number, significance) : Làm tròn xuống một số đến bội số gần nhất
GCD (number1, number2, ...) : Tìm ước số chung lớn nhất của các số
INT (number) : Làm tròn một số xuống số nguyên gần nhất
LCM (number1, number2, ...) : Tìm bội số chung nhỏ nhất của các số
LN (number) : Tính logarit tự nhiên của một số
LOG (number) : Tính logarit của một số
LOG10 (number) : Tính logarit cơ số 10 của một số
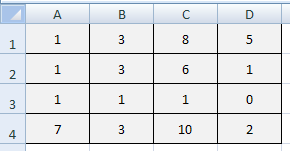
MDETERM (array) : Tính định thức của một ma trận
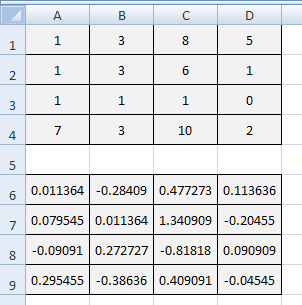
MINVERSE (array) : Tìm ma trận nghịch đảo của một ma trận
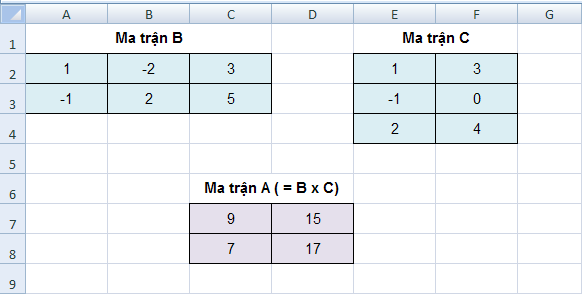
MMULT (array1, array2) : Tính tích hai ma trận
MOD (number, divisor) : Lấy phần dư của một phép chia.
MROUND (number, multiple) : Làm tròn một số đến bội số của một số khác
MULTINOMIAL (number1, number2, ...) : Tính tỷ lệ giữa giai thừa tổng và tích giai thừa các số
ODD (number): Làm tròn một số đến số nguyên lẻ gần nhất
PI () : Trả về giá trị con số Pi
POWER (number, power) : Tính lũy thừa của một số
PRODUCT(number1, number2, ...) : Tính tích các số
QUOTIENT (numberator, denominator) : Lấy phần nguyên của một phép chia
RAND () : Trả về một số ngẫu nhiên giữa 0 và 1
RANDBETWEEN (bottom, top) : Trả về một số ngẫu nhiên giữa một khoảng tùy chọn
ROMAN (number, form) : Chuyển một số (Ả-rập) về dạng số La-mã theo định dạng tùy chọn
ROUND (number, num_digits) : Làm tròn một số theo sự chỉ định
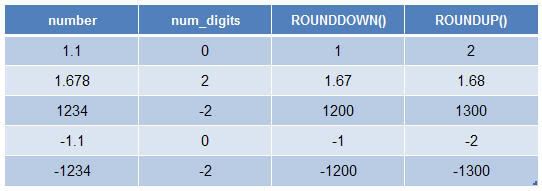
ROUNDDOWN (number, num_digits) : Làm tròn xuống một số theo sự chỉ định
ROUNDUP (number, num_digits) : Làm tròn lên một số theo sự chỉ định
SERIESSUM (x, n, m, coefficients) : Tính tổng lũy thừa của một chuỗi số
SIGN (number) : Trả về dấu (đại số) của một số
SQRT (number) : Tính căn bậc hai của một số
SQRTPI (number) : Tính căn bậc hai của một số được nhân với Pi
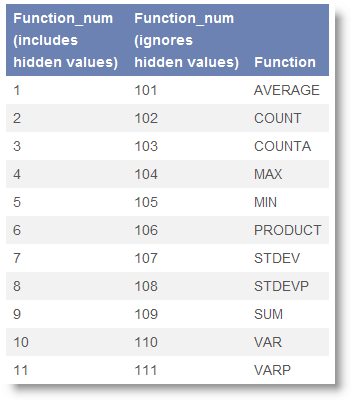
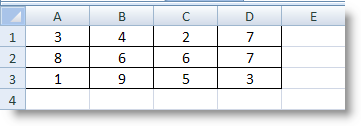
SUBTOTAL (function_num, ref1, ref2, ...) : Tính toán cho một nhóm con trong một danh sách tùy theo phép tính được chỉ định
SUM (number1, number2, ...) : Tính tổng các số
SUMIF (range, criteria, sum_range) : Tính tổng các ô thỏa một điều kiện chỉ định
SUMIFS (sum_range, criteria_range1, criteria1, criteria_range2, criteria2, …) : Tính tổng các ô thỏa nhiều điều kiện chỉ định[/URL]
SUMPRODUCT (array1, array2, ...) : Tính tổng các tích của các phần tử trong các mảng dữ liệu
SUMSQ (number1, number2, ...) : Tính tổng bình phương của các số
SUMX2MY2 (array_x, array_y) : Tính tổng của hiệu bình phương của các phần tử trong hai mảng giá trị
SUMX2PY2 (array_x, array_y) : Tính tổng của tổng bình phương của các phần tử trong hai mảng giá trị
SUMXMY2 (array_x, array_y) : Tính tổng của bình phương của hiệu các phần tử trong hai mảng giá trị
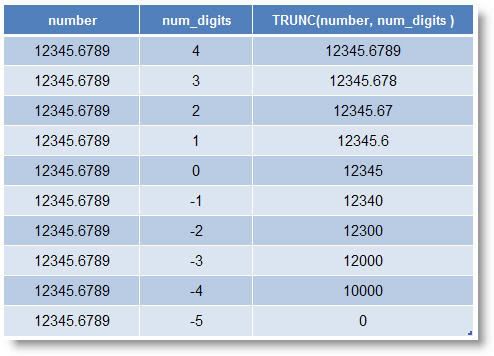
TRUNC (number, num_digits) : Lấy phần nguyên của một số (mà không làm tròn)
Danh mục các hàm toán học
ABS (number): Tính trị tuyệt đối của một số (giá trị tuyệt đối của một số là số luôn luôn dương).
CEILING (number, significance) : Làm tròn lên một số (cách xa khỏi số 0) đến bội số gần nhất của significance.
COMBIN (number, number_chosen) : Trả về số tổ hợp được chọn từ một số các phần tử. Thường dùng để xác định tổng số nhóm có được từ một số các phần tử.
EVEN (number) : Làm tròn một số đến số nguyên chẵn gần nhất
EXP (number) : Tính lũy thừa cơ số e của một số
FACT (number) : Tính giai thừa của một số
FACTDOUBLE (number) : Tính giai thừa cấp hai của một số
FLOOR (number, significance) : Làm tròn xuống một số đến bội số gần nhất
GCD (number1, number2, ...) : Tìm ước số chung lớn nhất của các số
INT (number) : Làm tròn một số xuống số nguyên gần nhất
LCM (number1, number2, ...) : Tìm bội số chung nhỏ nhất của các số
LN (number) : Tính logarit tự nhiên của một số
LOG (number) : Tính logarit của một số
LOG10 (number) : Tính logarit cơ số 10 của một số
MDETERM (array) : Tính định thức của một ma trận
MINVERSE (array) : Tìm ma trận nghịch đảo của một ma trận
MMULT (array1, array2) : Tính tích hai ma trận
MOD (number, divisor) : Lấy phần dư của một phép chia.
MROUND (number, multiple) : Làm tròn một số đến bội số của một số khác
MULTINOMIAL (number1, number2, ...) : Tính tỷ lệ giữa giai thừa tổng và tích giai thừa các số
ODD (number): Làm tròn một số đến số nguyên lẻ gần nhất
PI () : Trả về giá trị con số Pi
POWER (number, power) : Tính lũy thừa của một số
PRODUCT(number1, number2, ...) : Tính tích các số
QUOTIENT (numberator, denominator) : Lấy phần nguyên của một phép chia
RAND () : Trả về một số ngẫu nhiên giữa 0 và 1
RANDBETWEEN (bottom, top) : Trả về một số ngẫu nhiên giữa một khoảng tùy chọn
ROMAN (number, form) : Chuyển một số (Ả-rập) về dạng số La-mã theo định dạng tùy chọn
ROUND (number, num_digits) : Làm tròn một số theo sự chỉ định
ROUNDDOWN (number, num_digits) : Làm tròn xuống một số theo sự chỉ định
ROUNDUP (number, num_digits) : Làm tròn lên một số theo sự chỉ định
SERIESSUM (x, n, m, coefficients) : Tính tổng lũy thừa của một chuỗi số
SIGN (number) : Trả về dấu (đại số) của một số
SQRT (number) : Tính căn bậc hai của một số
SQRTPI (number) : Tính căn bậc hai của một số được nhân với Pi
SUBTOTAL (function_num, ref1, ref2, ...) : Tính toán cho một nhóm con trong một danh sách tùy theo phép tính được chỉ định
SUM (number1, number2, ...) : Tính tổng các số
SUMIF (range, criteria, sum_range) : Tính tổng các ô thỏa một điều kiện chỉ định
SUMIFS (sum_range, criteria_range1, criteria1, criteria_range2, criteria2, …) : Tính tổng các ô thỏa nhiều điều kiện chỉ định[/URL]
SUMPRODUCT (array1, array2, ...) : Tính tổng các tích của các phần tử trong các mảng dữ liệu
SUMSQ (number1, number2, ...) : Tính tổng bình phương của các số
SUMX2MY2 (array_x, array_y) : Tính tổng của hiệu bình phương của các phần tử trong hai mảng giá trị
SUMX2PY2 (array_x, array_y) : Tính tổng của tổng bình phương của các phần tử trong hai mảng giá trị
SUMXMY2 (array_x, array_y) : Tính tổng của bình phương của hiệu các phần tử trong hai mảng giá trị
TRUNC (number, num_digits) : Lấy phần nguyên của một số (mà không làm tròn)
Lần chỉnh sửa cuối: