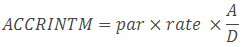- Tham gia
- 3/7/07
- Bài viết
- 4,946
- Được thích
- 23,213
- Nghề nghiệp
- Dạy đàn piano
Lời ngỏ:
Thú thật, khi dịch ý nghĩa cũng như cách sử dụng những hàm này, tôi gặp không ít lúng túng khi đụng đến những thuật ngữ liên quan đến tài chính.
Ví dụ: ... the security's price per $100 face value
Phải dịch là: Giá trị chứng khoán trên giá trị danh nghĩa của đồng $100
Hay là: Giá trị tính trên mỗi $100 của mệnh giá chứng khoán ?
Và:... the security's redemption value per $100 face valueHay là: Giá trị tính trên mỗi $100 của mệnh giá chứng khoán ?
Phải dịch là: Giá trị lấy lại được trên giá trị danh nghĩa của đồng $100
Hay là: Giá trị hoàn lại tính trên mỗi $100 ?
Hay là: Giá trị hoàn lại tính trên mỗi $100 ?
Thiết nghĩ cái giá trị của đồng $100 này, có lẽ chỉ thích hợp với đồng Dollar Mỹ, nên tạm thời tôi xin bỏ qua cái chuyện $100, chỉ xin tạm ghi là: "Giá trị chứng khoán" và "Giá trị hoàn lại" thôi...
Và từ "security", xin tạm hiểu là một chứng khoán, hay một khoản đầu tư, hay một khoản vay... tùy theo từng trường hợp.
Và còn nhiều thuật ngữ khác nữa...
Trong các bài sau đây, nếu gặp phải những sai sót, mong các bạn bỏ quá cho, và xin cứ góp ý thẳng với tôi để sửa lại cho đúng. Xin cảm ơn trước.
----------------------------------------------------------------------------------------------------
Hàm ACCRINT()
Tính lãi gộp cho một chứng khoán trả lãi theo định kỳ.
Cú pháp: = ACCRINT(issue, first_interest, settlement, rate, par, frequency, basis, calc_method)
Lưu ý:
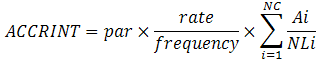
Ví dụ:
Issue : Ngày phát hành chứng khoán.
First_interest : Ngày tính lãi đầu tiên của chứng khoán.
Settlement : Ngày tới hạn của chứng khoán. Ngày này phải là một ngày sau ngày phát hành chứng khoán khi chứng khoán được giao dịch với người mua.
Rate : Lãi suất hằng năm của chứng khoán.
Par : Giá trị danh nghĩa của chứng khoán. Nếu bỏ qua, ACCRINT() sử dụng $1,000
Frequency : Số lần trả lãi hằng năm. Nếu trả mỗi năm một lần: frequency = 1; trả mỗi năm hai lần: frequency = 2; trả mỗi năm bốn lần: frequency = 4.
Basis : Là cơ sở dùng để đếm ngày (nếu bỏ qua, mặc định là 0)
First_interest : Ngày tính lãi đầu tiên của chứng khoán.
Settlement : Ngày tới hạn của chứng khoán. Ngày này phải là một ngày sau ngày phát hành chứng khoán khi chứng khoán được giao dịch với người mua.
Rate : Lãi suất hằng năm của chứng khoán.
Par : Giá trị danh nghĩa của chứng khoán. Nếu bỏ qua, ACCRINT() sử dụng $1,000
Frequency : Số lần trả lãi hằng năm. Nếu trả mỗi năm một lần: frequency = 1; trả mỗi năm hai lần: frequency = 2; trả mỗi năm bốn lần: frequency = 4.
Basis : Là cơ sở dùng để đếm ngày (nếu bỏ qua, mặc định là 0)
= 0 : Một tháng có 30 ngày / Một năm có 360 ngày (theo tiêu chuẩn Bắc Mỹ)
= 1 : Số ngày thực tế của mỗi tháng / Số ngày thực tế của mỗi năm
= 2 : Số ngày thực tế của mỗi tháng / Một năm có 360 ngày
= 3 : Số ngày thực tế của mỗi tháng / Một năm có 365 ngày
= 4 : Một tháng có 30 ngày / Một năm có 360 ngày (theo tiêu chuẩn Châu Âu)
Calc_method : Là một giá trị logic chỉ cách để tính số lãi gộp khi ngày kết toán chứng khoán (settlement) xảy ra sau ngày tính lãi đầu tiên của chứng khoán (fisrt_interest). Nếu là 1 (TRUE): số lãi gộp sẽ được tính từ ngày phát hành chứng khoán; nếu là 0 (FALSE): số lãi gộp sẽ chỉ tính từ ngày tính lãi đầu tiên của chứng khoán. Nếu bỏ qua, mặc định calc_method là 1.= 1 : Số ngày thực tế của mỗi tháng / Số ngày thực tế của mỗi năm
= 2 : Số ngày thực tế của mỗi tháng / Một năm có 360 ngày
= 3 : Số ngày thực tế của mỗi tháng / Một năm có 365 ngày
= 4 : Một tháng có 30 ngày / Một năm có 360 ngày (theo tiêu chuẩn Châu Âu)
Lưu ý:
- Nên dùng hàm DATE(year, month, day) khi nhập các giá trị ngày tháng.
- issue, first_interest, settlement, frequency và basis sẽ được cắt bỏ phần lẻ nếu chúng không phải là số nguyên
- Nếu issue, first_interest và settlement không là những ngày hợp lệ, ACCRINT() sẽ trả về giá trị lỗi #VALUE!
- Nếu rate ≤ 0 hay par ≤ 0, ACCRINT() sẽ trả về giá trị lỗi #NUM!
- Nếu frequency không phải là các con số 1, 2, hoặc 4, ACCRINT() sẽ trả về giá trị lỗi #NUM!
- Nếu basis < 0 hay basis > 4, ACCRINT() sẽ trả về giá trị lỗi #NUM!
- Nếu issue > settlement, ACCRINT() sẽ trả về giá trị lỗi #NUM!
- Hàm ACCRINT() sẽ tính toán theo công thức sau đây:
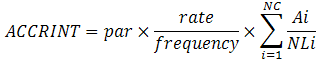
Với:
Ai : Số ngày tích lũy trong kỳ lãi thứ i với kỳ lẻ (1, 3, 5...)
NC : Số kỳ tính lãi thuộc kỳ lẻ. Nếu NC có phần lẻ thập phân, NC sẽ được làm tròn tới số nguyên kế tiếp
NLi : Số ngày bình thường trong kỳ tính lãi thứ i với kỳ lẻ
Ai : Số ngày tích lũy trong kỳ lãi thứ i với kỳ lẻ (1, 3, 5...)
NC : Số kỳ tính lãi thuộc kỳ lẻ. Nếu NC có phần lẻ thập phân, NC sẽ được làm tròn tới số nguyên kế tiếp
NLi : Số ngày bình thường trong kỳ tính lãi thứ i với kỳ lẻ
Ví dụ:
- Tính lãi gộp của một trái phiếu kho bạc có mệnh giá $1,000,000, phát hành ngày 1/3/2008, ngày tới hạn là 1/5/2009, ngày tính lãi đầu tiên là 31/8/2008 (tính lãi 6 tháng một lần) với lãi suất hằng năm là 10%, cơ sở để tính ngày là một năm 360 ngày, một tháng 30 ngày ?
= ACCRINT(DATE(2008,3,1), DATE(2008,8,31), DATE(2009,5,1), 10%, 1000000, 2, 0, TRUE) = $116,944.44
= ACCRINT(DATE(2008,3,1), DATE(2008,8,31), DATE(2009,5,1), 10%, 1000000, 2, 0, FALSE) = $116,667.67
Công thức trên tính tổng lãi gộp từ ngày phát hành trái phiếu, còn công thức dưới chỉ tính lãi gộp từ ngày đầu tiên bắt đầu tính lãi (31/8/2008)
= ACCRINT(DATE(2008,3,1), DATE(2008,8,31), DATE(2009,5,1), 10%, 1000000, 2, 0, FALSE) = $116,667.67
Công thức trên tính tổng lãi gộp từ ngày phát hành trái phiếu, còn công thức dưới chỉ tính lãi gộp từ ngày đầu tiên bắt đầu tính lãi (31/8/2008)
Chỉnh sửa lần cuối bởi điều hành viên: