quyenquyen@123
Thành viên mới

- Tham gia
- 24/8/23
- Bài viết
- 1
- Được thích
- 0
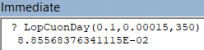
Một tấm vải hình chữ nhật có chiều rộng là 1,2m, chiều dài là 350m và được cuộn chặt xung quanh một lõi gỗ hình trụ có đường kinh 10cm liên tục cho đến hết, sao cho mép vải theo chiều rộng luôn song song với trục của hình trụ,Cho biết độ dày của cuộn vải đó sau khi đã cuộn hết tấm vải, biết rằng tấm vải có độ dày như nhau là 0,15mm (kết quả tỉnh theo xăng-ti-mét và làm tròn đến 3 chữ số thập phân)