You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
[Bài tập VBA cho người rỗi rảnh] Hãy viết 1 macro tìm ra 3 số nguyên tố liên tiếp (1 người xem)
- Thread starter SA_DQ
- Ngày gửi
Người dùng đang xem chủ đề này
Đang trực tuyến: 1 (Thành viên: 0, Khách: 1)
VetMini
Đang đi tìm hòn đá
- Tham gia
- 21/12/12
- Bài viết
- 17,867
- Được thích
- 24,788
- Nghề nghiệp
- Thầy bói bài ta
Hình như thớt diễn tả câu hỏi không rõ.Hai, ba, và năm. Đủ nhỉ?
Có lẽ muốn nói "các bộ ba số nguyên tố liên liếp"
2, 3, 5
3, 5, 7
5, 7, 11
...
(tìm các số nguyên tố nhỏ hơn hay bằng giới hạn)
Chú cho các quý vị muốn thử viết:
Bài này thuộc về giải thuật nhiều hơn code.
Upvote
0
Đối với câu đố này thì không cần VBA, chỉ cần thuộc định nghĩa số nguyên tố là gì rồi xòe bàn tay là thấy 3 con.Đáp án đúng, nhưng bài làm (các câu lệnh VBA) đâu vậy?!?
Có lẽ bài đố nên như sau:
- Hoặc là 3 số liên tiếp nhỏ hơn 600 nhưng gần 600 nhất
- Hoặc là liệt kê hết các bộ 3. (có trùng hoặc không trùng).
Hiển nhiên là không rõ ràng. Nếu tôi viết code để có 2, 3, 5 thì thủ thuật khác, nếu tôi viết code để lấy bộ 3 bất kỳ thì thủ thuật khác, nếu liệt kê hết các bộ 3 thì thủ thuật lại khác nữa. Nếu lấy bộ 3 gần 600 nhất, thì lại khác nữa.Hình như thớt diễn tả câu hỏi không rõ.
Có lẽ muốn nói "các bộ ba số nguyên tố liên liếp"
Thứ hai, một câu đố mà giải ra kết quả nào cũng đúng thì không phải là câu đố chuẩn.
Upvote
0
Thuật toán Capilot:
Đây là hướng dẫn từng bước về cách bạn có thể tìm ba số nguyên tố liên tiếp với ba chữ số:
Đây là hướng dẫn từng bước về cách bạn có thể tìm ba số nguyên tố liên tiếp với ba chữ số:
- Hiểu về số nguyên tố:
- Số nguyên tố là số tự nhiên lớn hơn 1 và chỉ chia hết cho 1 và chính nó.
- Xác định phạm vi:
- Bạn cần tìm các số nguyên tố có ba chữ số, vì vậy chúng nên nằm trong khoảng từ 100 đến 999.
- Kiểm tra từng số:
- Bắt đầu từ 100 và kiểm tra từng số xem có phải là số nguyên tố hay không. Bạn có thể sử dụng phương pháp chia thử, tức là chia số đó cho từng số nguyên từ 2 đến căn bậc hai của nó. Nếu tất cả các phép chia này không cho kết quả là số nguyên, thì số đó là số nguyên tố.
- Tìm các số nguyên tố liên tiếp:
- Sau khi bạn tìm thấy số nguyên tố ba chữ số đầu tiên (là 101), tiếp tục đến số tiếp theo (102) và kiểm tra xem nó có phải là số nguyên tố không. Nếu không, chuyển sang số tiếp theo (103) và tiếp tục cho đến khi bạn tìm thấy ba số nguyên tố liên tiếp.
Marco Capilot:
Mã:Sub FindConsecutivePrimes() Dim count As Integer Dim num As Integer Dim primes(2) As Integer count = 0 num = 100 Do While count < 3 If IsPrime(num) Then primes(count) = num count = count + 1 End If num = num + 1 Loop ' In ra ba số nguyên tố liên tiếp For i = 0 To 2 Debug.Print primes(i) Next i End Sub Function IsPrime(n As Integer) As Boolean Dim i As Integer If n <= 1 Then IsPrime = False Exit Function End If For i = 2 To Int(Sqr(n)) If n Mod i = 0 Then IsPrime = False Exit Function End If Next i IsPrime = True End Function
- Sau khi bạn tìm thấy số nguyên tố ba chữ số đầu tiên (là 101), tiếp tục đến số tiếp theo (102) và kiểm tra xem nó có phải là số nguyên tố không. Nếu không, chuyển sang số tiếp theo (103) và tiếp tục cho đến khi bạn tìm thấy ba số nguyên tố liên tiếp.
File đính kèm
Lần chỉnh sửa cuối:
Upvote
0
VetMini
Đang đi tìm hòn đá
- Tham gia
- 21/12/12
- Bài viết
- 17,867
- Được thích
- 24,788
- Nghề nghiệp
- Thầy bói bài ta
Điểm code để người khác chấm. Tôi chỉ chấm điểm thuật toán:
1. Nếu chỉ theo đúng chỉ dẫn 3 của bài #7: tối đa 7/10 điểm
2. Áp dụng các thuật toán, mẹo, đặc điểm của ngôn ngữ để ưu hóa: tối đa 10/10 điểm.
Đó là theo đề bài sửa lại ở bài #6.
Nếu sửa đề bài theo bài #4 thì còn một thuật toán ưu việt nữa. (nói như vậy là tôi đã gợi ý rồi đấy)
1. Nếu chỉ theo đúng chỉ dẫn 3 của bài #7: tối đa 7/10 điểm
2. Áp dụng các thuật toán, mẹo, đặc điểm của ngôn ngữ để ưu hóa: tối đa 10/10 điểm.
Đó là theo đề bài sửa lại ở bài #6.
Nếu sửa đề bài theo bài #4 thì còn một thuật toán ưu việt nữa. (nói như vậy là tôi đã gợi ý rồi đấy)
Upvote
0
Tôi thì cho CoPilot 7 điểm, người làm theo chỉ 2 điểm. Không làm theo mà copy code về chạy thì cho ốc zịt.1. Nếu chỉ theo đúng chỉ dẫn 3 của bài #7: tối đa 7/10 điểm
Upvote
0
- Tham gia
- 8/6/06
- Bài viết
- 14,776
- Được thích
- 23,229
- Nghề nghiệp
- U80
Có 1 tính chất của các SNT (số nguyên tố) lớn hơn 100 là toàn số lẻ
Như vậy bài toán có thể rút ngắn gần phân nữa đoạn đường nhờ khảo sát chỉ những số lẽ 101, 103,. . . .,999
Để snh động hơn, ta có thể tìm số lẽ N bất kỳ trong khoảng 101.. 505 & bắt đầu tìm 3 SNT liền kề ( > N) từ N này
Như vậy bài toán có thể rút ngắn gần phân nữa đoạn đường nhờ khảo sát chỉ những số lẽ 101, 103,. . . .,999
Để snh động hơn, ta có thể tìm số lẽ N bất kỳ trong khoảng 101.. 505 & bắt đầu tìm 3 SNT liền kề ( > N) từ N này
Upvote
0
VetMini
Đang đi tìm hòn đá
- Tham gia
- 21/12/12
- Bài viết
- 17,867
- Được thích
- 24,788
- Nghề nghiệp
- Thầy bói bài ta
Đúng. Vì vậy thuật toán xét đã được ưu hóa là xét xem nó có phải là số lẻ trước. Lúc xét chia chẵn thì cũng chỉ xét chia cho số lẻ (từ 3 đến căn hai số step 2)Có 1 tính chất của các SNT (số nguyên tố) lớn hơn 100 là toàn số lẻ
Như vậy bài toán có thể rút ngắn gần phân nữa đoạn đường nhờ khảo sát chỉ những số lẽ 101, 103,. . . .,999
Để snh động hơn, ta có thể tìm số lẽ N bất kỳ trong khoảng 101.. 505 & bắt đầu tìm 3 SNT liền kề ( > N) từ N này
Function IsPrime(n As Long) As Boolean
IsPrime = True
Select Case n
Case 0, 1 ???? ' tùy theo định nghĩa mà là nguyên tố hay không?
Case 2
Exit Function
Case Else
If (n And 1) = 0 Then ' số chẵn
IsPrime = False
Exit Function
End If
For i = 3 To Sqrt(n) Step 2
If n % i = 0 Then
IsPrime = False
Exit Function
End If
Next i
End Select
End Function
Chú cho những người quên toán số học cấp 2:
Tại sao chỉ xét đến sqrt(n)?
Lô gic toán: nếu i chia chẵn n thì có một số j sao cho n = i*j
Số j này cũng chia chẵn n
nếu i < sqrt(n) thì j > sqrt(i) và ngược lại.
Vì vậy chỉ cần xét chia chẵn đến sqrt(n) bởi vì j đã được ngầm xét rồi.
Tại sao tôi đề nghị đề bài mở rộng thêm ở chỗ bài #4?
Upvote
0
HUONGHCKT
Zalo 0986997214
Xin được góp vui và rất mong nhận được nhiều góp ý để nâng cao kiến thứcCó 1 tính chất của các SNT (số nguyên tố) lớn hơn 100 là toàn số lẻ
Như vậy bài toán có thể rút ngắn gần phân nữa đoạn đường nhờ khảo sát chỉ những số lẽ 101, 103,. . . .,999
Để snh động hơn, ta có thể tìm số lẽ N bất kỳ trong khoảng 101.. 505 & bắt đầu tìm 3 SNT liền kề ( > N) từ N này
Mã:
Option Explicit
Public t&, KQ()
Sub SoNguyenTo(ByVal S1 As Long, S2 As Long, Chon As Integer)
'Chon =1 lay tât ca cac sô nguyen tô tim đươc thành 1 cot
'Chon=2 lay 1 tap gôm 3 sô nguyên to liên kê
'Chon = 3 lay 1 tâp gôm nhiêu tâp 3 sô nguyên to liên kê xêp vào 1 côt
Dim i&, j&, k&, a&, N&, Nhay&, SN&
Dim S, L
S = Array(2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37)
ReDim KQ(1 To (S2 - S1), 1 To 1)
SN = SoNgauNghien(S1, S2)
t = 0
If SN = 1 Then SN = 2
If SN >= 100 Then
If SN Mod 2 = 0 Then SN = SN + 1
Nhay = 2
Else
Nhay = 1
End If
For i = SN To S2 Step Nhay
For j = LBound(S) To UBound(S)
If i = S(j) Or i Mod S(j) <> 0 Then N = 1 Else N = 0: Exit For
Next j
If N = 1 Then
Select Case Chon
Case Is = 1
t = t + 1: KQ(t, 1) = i
Case Is = 2
a = a + 1: If L = Empty Then L = i Else L = L & ";" & i
If a = 3 Then t = t + 1: KQ(t, 1) = L: Exit For
Case Is = 3
a = a + 1: If L = Empty Then L = i Else L = L & ";" & i
If a Mod 3 = 0 Then t = t + 1: KQ(t, 1) = L: L = Empty
End Select
End If
Next i
End Sub
Sub Test()
Call SoNguyenTo(100, 999, 3)
Sheet2.[A10].Resize(1000, 1).ClearContents
Sheet2.[A10].Resize(t, 1) = KQ
End Sub
Function SoNgauNghien(iMin As Long, iMax As Long)
Call Randomize
SoNgauNghien = Int((iMax - iMin + 1) * Rnd + iMin)
End Function*.2 tham số đầu là Từ số...., đến số và bắt đầu tìm từ 1 số ngẫu nghiên nằm trong khoảng Từ ...đến...,
*.tham số thứ 3 là:
Nếu Chon=1 :Kết quả trả về là 1 tập gồm tất cả các CNT tìm được gán vào 1 cột
Nếu Chon= 2: Kết quả trả về là 1 tập gồm 3 số NT liền kề cách nhau bởi dấu ";"
Nếu Chon=3: Kết quả trả về là 1 tập gồm nhiều tập Con có 3 số NT liền kề cách nhau bởi dấu ";"
Lần chỉnh sửa cuối:
Upvote
0
VetMini
Đang đi tìm hòn đá
- Tham gia
- 21/12/12
- Bài viết
- 17,867
- Được thích
- 24,788
- Nghề nghiệp
- Thầy bói bài ta
Tuy sinh động nhưng nó liên quan đến loại toán khác, không nằm trong tinh thần "số nguyên tố",Có 1 tính chất của các SNT (số nguyên tố) lớn hơn 100 là toàn số lẻ
Như vậy bài toán có thể rút ngắn gần phân nữa đoạn đường nhờ khảo sát chỉ những số lẽ 101, 103,. . . .,999
Để snh động hơn, ta có thể tìm số lẽ N bất kỳ trong khoảng 101.. 505 & bắt đầu tìm 3 SNT liền kề ( > N) từ N này
Bài toán tôi đề nghị ở bài #4 là một loại triển khai đặc tính nguyên tố. Gợi ý đến đây là gần hết cái thuật toán mà tôi muốn nói rồi.
Upvote
0
Nếu trong khoảng từ 101 đến 999 có n số nguyên tố, thì giải bài 4 sẽ được n - 2 bộ 3 liền kề. Vẫn phải liệt kê hết n số ra rồi mới ghép bộ, và quá trình liệt kê vẫn phải dựa vào định nghĩa (đặc tính) số nguyên tố rồi. Ý anh cũng không rõ ràng như bài 1 vậy á.Bài toán tôi đề nghị ở bài #4 là một loại triển khai đặc tính nguyên tố. Gợi ý đến đây là gần hết cái thuật toán mà tôi muốn nói rồi.
Còn giải thuật thì cũng chỉ là vònglặp với step 2. Hoặc giải thuật khác cũng vậy, không giúp gì cho việc liệt kê hết n số tốt hơn.
À còn 1 ý nữa, số (2 ký số trở lên) tận cùng là 5 cũng là số lẻ nhưng không phải số nguyên tố, có thể bỏ qua để giảm thiểu số vòng lặp.
Lần chỉnh sửa cuối:
Upvote
0
VetMini
Đang đi tìm hòn đá
- Tham gia
- 21/12/12
- Bài viết
- 17,867
- Được thích
- 24,788
- Nghề nghiệp
- Thầy bói bài ta
Không phải vậy.Nếu trong khoảng từ 101 đến 999 có n số nguyên tố, thì giải bài 4 sẽ được n - 2 bộ 3 liền kề. Vẫn phải liệt kê hết n số ra rồi mới ghép bộ, và quá trình liệt kê vẫn phải dựa vào định nghĩa (đặc tính) số nguyên tố rồi. Ý anh cũng không rõ ràng như bài 1 vậy á.
Còn giải thuật thì cũng chỉ là vònglặp với step 2. Hoặc giải thuật khác cũng vậy, không giúp gì cho việc liệt kê hết n số tốt hơn.
À còn 1 ý nữa, số (2 ký số trở lên) tận cùng là 5 cũng là số lẻ nhưng không phải số nguyên tố, có thể bỏ qua để giảm thiểu số vòng lặp.
Xét xem môt số có phải là nguyên tố và xét xem có bao nhiêu số nguyên tố từ 1 đến k dùng giải thuật khác nhau.
Cũng toán số cấp 2:
Lúc mò xem một số có phải là nguyên tố, ta chỉ cần chia thử cho các số nguyên tố nhỏ hơn hay bằng căn hai nó.
Vì vậy:
Nếu phải tìm tất cả các số nguyên tố từ 1 thì ta có thể chép các kết quả tuần tự vào một mảng. Lúc thử số kế tiếp thì lôi mảng này ra mà chia.
Đây là kỹ thuật dùng "sàng số nguyên tố", kỹ thuật kia là "trâu bò/ brute force cải tiến".
Khi vùng giới hạn k1~k2 có đặc tính k1 khá nhỏ và k2 khá lớn thì kỹ thuật sàng số nhanh hơn hẳn. Mặc dù phải phí một mớ năng lượng để fill mảng từ 1 đến k1.
Upvote
0
Vụ này giờ tôi mới biết. Cấp 2, cấp 3 đều không có dạy. Tôi học lớp 6 năm 1972, lớp 6, 7, 8 học chương trình trước giải phóng, qua lớp 9 là chương trình sau giải phóng mà không có cái này. Giới hạn chia thử là căn 2 thì tôi tự suy luận ra chứ trường cũng không dạy.Cũng toán số cấp 2:
Lúc mò xem một số có phải là nguyên tố, ta chỉ cần chia thử cho các số nguyên tố nhỏ hơn hay bằng căn hai nó.
Upvote
0
VetMini
Đang đi tìm hòn đá
- Tham gia
- 21/12/12
- Bài viết
- 17,867
- Được thích
- 24,788
- Nghề nghiệp
- Thầy bói bài ta
Có lẽ do bà cô dạy toán của tôi thêm vào. Bả dạy như bài tập thức hành cho hệ luận:Vụ này giờ tôi mới biết. Cấp 2, cấp 3 đều không có dạy. Tôi học lớp 6 năm 1972, lớp 6, 7, 8 học chương trình trước giải phóng, qua lớp 9 là chương trình sau giải phóng mà không có cái này. Giới hạn chia thử là căn 2 thì tôi tự suy luận ra chứ trường cũng không dạy.
Mọi số không nguyên tố đều là tích nhân của nhiều số nguyên tố nhỏ hơn nó.
Chú:
Tôi để ý thấy bài #12 có theo giải thuật "sàng nguyên tố". Tức là bạn này có biết qua.
Nhắn tác giả lài #12:
1. sàng của bạn có số 9, không phải là nguyên tố.
2. khi code dài và phức tạp. Bạn nên đặt tên tham theo kiểu khác với biến nội, dễ đọc và chơn. Đọc bài của bạn, tôi cứ bị nhầm S, S1, S2 đều là biến nội trong khi thực tế chỉ có S là biến nội
3. khi code dùng nhiều đến mảng thì đặt mảng một chiều thay vì hai chiều mà các chỉ số cột đều là 1 thì code chạy không hiệu quả (con tính địa chỉ phần tử của mảng 1 chiều nhanh hơn 2 chiếu). Lúc cần thì dùng hàm INDEX và TRANSPOSE chỉnh lại.
Lần chỉnh sửa cuối:
Upvote
0
À phải, tôi có đọc câu này (nguyên văn) nhưng không để ý vì nó nằm trong bài toán khác: Phân tích 1 số thành các thừa số nguyên tố, áp dụng trong việc tìm ước số chung lớn nhất.Có lẽ do bà cô dạy toán của tôi thêm vào. Bả dạy như bài tập thức hành cho hệ luận:
Mọi số không nguyên tố đều là tích nhân của nhiều số nguyên tố nhỏ hơn nó.
Upvote
0
HUONGHCKT
Zalo 0986997214
Cảm ơn anh đã chỉ bảo.Có lẽ do bà cô dạy toán của tôi thêm vào. Bả dạy như bài tập thức hành cho hệ luận:
Mọi số không nguyên tố đều là tích nhân của nhiều số nguyên tố nhỏ hơn nó.
Chú:
Tôi để ý thấy bài #12 có theo giải thuật "sàng nguyên tố". Tức là bạn này có biết qua.
Nhắn tác giả lài #12:
1. sàng của bạn có số 9, không phải là nguyên tố.
2. khi code dài và phức tạp. Bạn nên đặt tên tham theo kiểu khác với biến nội, dễ đọc và chơn. Đọc bài của bạn, tôi cứ bị nhầm S, S1, S2 đều là biến nội trong khi thực tế chỉ có S là biến nội
3. khi code dùng nhiều đến mảng thì đặt mảng một chiều thay vì hai chiều mà các chỉ số cột đều là 1 thì code chạy không hiệu quả (con tính địa chỉ phần tử của mảng 1 chiều nhanh hơn 2 chiếu). Lúc cần thì dùng hàm INDEX và TRANSPOSE chỉnh lại.
Đúng là Tôi đã viết thừa số 9 trong mảng các số nguyên tố đầu tiên.
Upvote
0
- Tham gia
- 8/6/06
- Bài viết
- 14,776
- Được thích
- 23,229
- Nghề nghiệp
- U80
Mình lập 1 bảng các số nguyên tố như dưới đây & mong các bạn góp ý thêm:
PHP:
Sub BangSoNguyenTo111_999()
Dim Rw As Integer, Col As Integer, Num As Integer, Cot As Integer, RwMax As Integer
ReDim Arr(1 To 50, 1 To 9) As Integer
[A1].Resize(50, 9).Value = Space(0)
For Num = 101 To 999 Step 2
If IsPrime(Num) Then
Col = Num \ 100
If Col > Cot Then
If Rw > RwMax Then RwMax = Rw
Cot = Col: Rw = 1
Else
Rw = Rw + 1
End If
Arr(Rw, Col) = Num
End If
Next Num
[A1].Resize(RwMax, 9).Value = Arr()
End Sub
Mã:
Function IsPrime(n As Integer) As Boolean
Dim i As Integer
For i = 2 To Sqr(n)
If n Mod i = 0 Then
IsPrime = False: Exit Function
End If
Next i
IsPrime = True
End Function
Upvote
0
Châu Bá Thông
Trí tuệ trong trẻo - nghịch ngợm vô biên
- Tham gia
- 19/12/08
- Bài viết
- 115
- Được thích
- 325
- Nghề nghiệp
- Đốn củi
Function IsPrime(n As Long) As Boolean
If n <= 1 Then
IsPrime = False
Exit Function
End If
If n = 2 Then
IsPrime = True
Exit Function
End If
If n Mod 2 = 0 Then
IsPrime = False
Exit Function
End If
For i = 3 To Int(Sqr(n)) Step 2
If n Mod i = 0 Then
IsPrime = False
Exit Function
End If
Next i
IsPrime = True
End Function
Sub FindConsecutivePrimes()
Dim primes() As Long
Dim count As Long
Dim n As Long
Dim i As Long
Dim ws As Worksheet
Dim outputRow As Long
' Chuẩn bị trang tính để xuất kết quả
Set ws = ThisWorkbook.Sheets("Sheet1")
ws.Cells.ClearContents
ws.Range("A1:C1") = Array("Prime 1", "Prime 2", "Prime 3")
outputRow = 2
' Tìm các số nguyên tố từ 101 đến 997
ReDim primes(1 To 1)
count = 0
For n = 101 To 997 Step 2
If IsPrime(n) Then
count = count + 1
If count > UBound(primes) Then ReDim Preserve primes(1 To count + 100)
primes(count) = n
End If
Next n
ReDim Preserve primes(1 To count)
' Kiểm tra và xuất các bộ ba số nguyên tố liên tiếp
If count < 3 Then
ws.Range("A2").Value = "Không tìm thấy bộ ba nào."
Exit Sub
End If
For i = 1 To count - 2
ws.Cells(outputRow, 1).Value = primes(i)
ws.Cells(outputRow, 2).Value = primes(i + 1)
ws.Cells(outputRow, 3).Value = primes(i + 2)
outputRow = outputRow + 1
Next i
MsgBox "Đã tìm thấy " & (count - 2) & " bộ ba số nguyên tố liên tiếp.", vbInformation
End Sub
If n <= 1 Then
IsPrime = False
Exit Function
End If
If n = 2 Then
IsPrime = True
Exit Function
End If
If n Mod 2 = 0 Then
IsPrime = False
Exit Function
End If
For i = 3 To Int(Sqr(n)) Step 2
If n Mod i = 0 Then
IsPrime = False
Exit Function
End If
Next i
IsPrime = True
End Function
Sub FindConsecutivePrimes()
Dim primes() As Long
Dim count As Long
Dim n As Long
Dim i As Long
Dim ws As Worksheet
Dim outputRow As Long
' Chuẩn bị trang tính để xuất kết quả
Set ws = ThisWorkbook.Sheets("Sheet1")
ws.Cells.ClearContents
ws.Range("A1:C1") = Array("Prime 1", "Prime 2", "Prime 3")
outputRow = 2
' Tìm các số nguyên tố từ 101 đến 997
ReDim primes(1 To 1)
count = 0
For n = 101 To 997 Step 2
If IsPrime(n) Then
count = count + 1
If count > UBound(primes) Then ReDim Preserve primes(1 To count + 100)
primes(count) = n
End If
Next n
ReDim Preserve primes(1 To count)
' Kiểm tra và xuất các bộ ba số nguyên tố liên tiếp
If count < 3 Then
ws.Range("A2").Value = "Không tìm thấy bộ ba nào."
Exit Sub
End If
For i = 1 To count - 2
ws.Cells(outputRow, 1).Value = primes(i)
ws.Cells(outputRow, 2).Value = primes(i + 1)
ws.Cells(outputRow, 3).Value = primes(i + 2)
outputRow = outputRow + 1
Next i
MsgBox "Đã tìm thấy " & (count - 2) & " bộ ba số nguyên tố liên tiếp.", vbInformation
End Sub
Upvote
0
Châu Bá Thông
Trí tuệ trong trẻo - nghịch ngợm vô biên
- Tham gia
- 19/12/08
- Bài viết
- 115
- Được thích
- 325
- Nghề nghiệp
- Đốn củi
Function IsPrime(n As Long, ByRef primes As Collection) As Boolean
Dim i As Long
Dim sq As Double
' Kiểm tra nhanh các trường hợp cơ bản
If n <= 1 Then
IsPrime = False
Exit Function
End If
If n = 2 Then
IsPrime = True
Exit Function
End If
If n Mod 2 = 0 Then
IsPrime = False
Exit Function
End If
' Kiểm tra chia hết với các số nguyên tố đã lưu
sq = Sqr(n)
For Each i In primes
If i > sq Then Exit For
If n Mod i = 0 Then
IsPrime = False
Exit Function
End If
Next i
' Nếu không chia hết thì là số nguyên tố
IsPrime = True
If IsPrime Then primes.Add n ' Thêm vào danh sách các số nguyên tố
End Function
Sub FindConsecutivePrimes()
Dim primes As New Collection
Dim n As Long
Dim i As Long
Dim ws As Worksheet
Dim outputRow As Long
Dim result As Variant
Dim idx As Long
' Chuẩn bị trang tính để xuất kết quả
Set ws = ThisWorkbook.Sheets("Sheet1")
ws.Cells.ClearContents
ws.Range("A1:C1").Value = Array("Prime 1", "Prime 2", "Prime 3")
outputRow = 2
' Tìm các số nguyên tố từ 101 đến 997
For n = 101 To 997 Step 2
Call IsPrime(n, primes)
Next n
' Xuất các bộ ba số nguyên tố liên tiếp
If primes.Count < 3 Then
ws.Range("A2").Value = "Không tìm thấy bộ ba nào."
Exit Sub
End If
ReDim result(1 To primes.Count - 2, 1 To 3)
For i = 1 To primes.Count - 2
result(i, 1) = primes(i)
result(i, 2) = primes(i + 1)
result(i, 3) = primes(i + 2)
Next i
ws.Range(ws.Cells(outputRow, 1), ws.Cells(outputRow + UBound(result, 1) - 1, 3)).Value = result
MsgBox "Đã tìm thấy " & (primes.Count - 2) & " bộ ba số nguyên tố liên tiếp.", vbInformation
End Sub
Thử lại
Dim i As Long
Dim sq As Double
' Kiểm tra nhanh các trường hợp cơ bản
If n <= 1 Then
IsPrime = False
Exit Function
End If
If n = 2 Then
IsPrime = True
Exit Function
End If
If n Mod 2 = 0 Then
IsPrime = False
Exit Function
End If
' Kiểm tra chia hết với các số nguyên tố đã lưu
sq = Sqr(n)
For Each i In primes
If i > sq Then Exit For
If n Mod i = 0 Then
IsPrime = False
Exit Function
End If
Next i
' Nếu không chia hết thì là số nguyên tố
IsPrime = True
If IsPrime Then primes.Add n ' Thêm vào danh sách các số nguyên tố
End Function
Sub FindConsecutivePrimes()
Dim primes As New Collection
Dim n As Long
Dim i As Long
Dim ws As Worksheet
Dim outputRow As Long
Dim result As Variant
Dim idx As Long
' Chuẩn bị trang tính để xuất kết quả
Set ws = ThisWorkbook.Sheets("Sheet1")
ws.Cells.ClearContents
ws.Range("A1:C1").Value = Array("Prime 1", "Prime 2", "Prime 3")
outputRow = 2
' Tìm các số nguyên tố từ 101 đến 997
For n = 101 To 997 Step 2
Call IsPrime(n, primes)
Next n
' Xuất các bộ ba số nguyên tố liên tiếp
If primes.Count < 3 Then
ws.Range("A2").Value = "Không tìm thấy bộ ba nào."
Exit Sub
End If
ReDim result(1 To primes.Count - 2, 1 To 3)
For i = 1 To primes.Count - 2
result(i, 1) = primes(i)
result(i, 2) = primes(i + 1)
result(i, 3) = primes(i + 2)
Next i
ws.Range(ws.Cells(outputRow, 1), ws.Cells(outputRow + UBound(result, 1) - 1, 3)).Value = result
MsgBox "Đã tìm thấy " & (primes.Count - 2) & " bộ ba số nguyên tố liên tiếp.", vbInformation
End Sub
Bài đã được tự động gộp:
Thử lại
PHP:
Function GeneratePrimes(maxNumber As Long) As Long()
' Tạo sàng Eratosthenes để lọc số nguyên tố đến maxNumber
Dim sieve() As Boolean
Dim primes() As Long
Dim i As Long, j As Long, count As Long
ReDim sieve(2 To maxNumber)
For i = 2 To maxNumber
sieve(i) = True
Next i
For i = 2 To Int(Sqr(maxNumber))
If sieve(i) Then
For j = i * i To maxNumber Step i
sieve(j) = False
Next j
End If
Next i
' Đếm số nguyên tố trong khoảng 101-999
count = 0
For i = 101 To maxNumber - 2 ' Đảm bảo có 3 số liên tiếp
If sieve(i) And sieve(i + 2) And sieve(i + 4) Then
count = count + 1
End If
Next i
' Lưu các bộ ba số nguyên tố liên tiếp
ReDim primes(1 To count, 1 To 3)
count = 0
For i = 101 To maxNumber - 2
If sieve(i) And sieve(i + 2) And sieve(i + 4) Then
count = count + 1
primes(count, 1) = i
primes(count, 2) = i + 2
primes(count, 3) = i + 4
End If
Next i
GeneratePrimes = primes
End Function
PHP:
Sub FindConsecutivePrimesOptimized()
Dim primes() As Long
Dim ws As Worksheet
Dim startTime As Double
startTime = Timer
Set ws = ThisWorkbook.Sheets("Sheet1")
ws.Cells.ClearContents
ws.Range("A1:C1") = Array("Prime 1", "Prime 2", "Prime 3")
' Tạo danh sách số nguyên tố và xuất kết quả
primes = GeneratePrimes(999)
If UBound(primes, 1) >= 1 Then
ws.Range("A2").Resize(UBound(primes, 1), 3).Value = primes
MsgBox "Tìm thấy " & UBound(primes, 1) & " bộ ba." & vbCrLf & _
"Thời gian chạy: " & Format(Timer - startTime, "0.000") & " giây.", vbInformation
Else
MsgBox "Không tìm thấy bộ ba nào.", vbExclamation
End If
End Sub
Lần chỉnh sửa cuối:
Upvote
0
Châu Bá Thông
Trí tuệ trong trẻo - nghịch ngợm vô biên
- Tham gia
- 19/12/08
- Bài viết
- 115
- Được thích
- 325
- Nghề nghiệp
- Đốn củi
Thử lại lần cuối, tùy chọn vùng kiểm tra minNumber (>=2), maxNumber do người dùng tự quyết định, ví dụ này là minNumber = 101, maxNumber =999
PHP:
Function GeneratePrimes(minNumber as Long, maxNumber As Long) As Long()
' Tạo sàng Eratosthenes để lọc số nguyên tố đến maxNumber
Dim sieve() As Boolean
Dim primesList() As Long
Dim tripletArray() As Long
Dim i As Long, j As Long
Dim primeCount As Long, tripletCount As Long
' Khởi tạo sàng
ReDim sieve(2 To maxNumber)
For i = 2 To maxNumber
sieve(i) = True
Next i
For i = 2 To Int(Sqr(maxNumber))
If sieve(i) Then
For j = i * i To maxNumber Step i
sieve(j) = False
Next j
End If
Next i
' Lọc các số nguyên tố trong khoảng minNumber-maxNumber
primeCount = 0
For i = minNumber To maxNumber
If sieve(i) Then primeCount = primeCount + 1
Next i
If primeCount = 0 Then
GeneratePrimes = Array()
Exit Function
End If
' Lưu vào mảng primesList
ReDim primesList(1 To primeCount)
primeCount = 0
For i = minNumber To maxNumber
If sieve(i) Then
primeCount = primeCount + 1
primesList(primeCount) = i
End If
Next i
' Tìm các bộ ba liên tiếp trong danh sách
tripletCount = 0
For i = 1 To primeCount - 2
tripletCount = tripletCount + 1
Next i
If tripletCount = 0 Then
GeneratePrimes = Array()
Exit Function
End If
' Lưu kết quả vào mảng 2D
ReDim tripletArray(1 To tripletCount, 1 To 3)
For i = 1 To tripletCount
tripletArray(i, 1) = primesList(i)
tripletArray(i, 2) = primesList(i + 1)
tripletArray(i, 3) = primesList(i + 2)
Next i
GeneratePrimes = tripletArray
End Function
'---------------------------------------------------------
Sub FindConsecutivePrimesOptimized()
Dim primes() As Long
Dim ws As Worksheet
Dim startTime As Double
startTime = Timer
Set ws = ThisWorkbook.Sheets("Sheet1")
ws.Cells.ClearContents
ws.Range("A1:C1") = Array("Prime 1", "Prime 2", "Prime 3")
primes = GeneratePrimes(101,999) '****
If Not IsEmpty(primes) Then
ws.Range("A2").Resize(UBound(primes, 1), 3).Value = primes
MsgBox "Tìm thấy " & UBound(primes, 1) & " bộ ba." & vbCrLf & _
"Thời gian chạy: " & Format(Timer - startTime, "0.000") & " giây.", vbInformation
Else
MsgBox "Không tìm thấy bộ ba nào.", vbExclamation
End If
End Sub
Lần chỉnh sửa cuối:
Upvote
0
- Tham gia
- 8/6/06
- Bài viết
- 14,776
- Được thích
- 23,229
- Nghề nghiệp
- U80
TẠO BẢNG 100 SỐ NGUYÊN TỐ GỒM 3 KÝ SỐ LỚN NHẤT.
PHP:
Sub TaoBang100SoNguyenTo3ChuSoLonNhat()
Dim Num As Integer, Col As Integer, Cot As Integer, Rw As Integer, Dem As Integer
ReDim Arr(1 To 30, 1 To 9) As String: Dim RwMax As Integer
Sheet2.Select
[B2].Resize(30, 9).Value = Arr(): Cot = 9
For Num = 999 To 101 Step -2
If IsPrime(Num) Then
Col = Num \ 100
If Col < Cot Then
If Rw > RwMax Then RwMax = Rw
Cot = Col: Rw = 1
Else
Rw = Rw + 1
End If
Arr(Rw, Col) = CStr(Num): Dem = Dem + 1
If Dem = 100 Then
[B2].Resize(RwMax, 9).Value = Arr(): Exit Sub
End If
End If
Next Num
End SubHàm IsPrime(Num) đã có ở #21.
Lần chỉnh sửa cuối:
Upvote
0
Thêm giải pháp Query:
1. Tạo 1 function để kiếm tra 1 số xem có thỏa là số nguyên tố không? --> True/false
2. Dùng List.Generate ( tương tự vòng lặp for trong vba ) để duyệt từ 997 xuống mỗi lần trừ 2, nếu true thì gán vào List,
3. Lấy n số từ đầu danh sách bằng List.FirstN
1. Tạo 1 function để kiếm tra 1 số xem có thỏa là số nguyên tố không? --> True/false
Mã:
//fNguyenTo
(so as number) as logical =>
let
kq= List.Count(List.Select({2..Number.RoundDown(Number.Sqrt(so))}, each Number.Mod(so, _) = 0 )) = 0
in
kq2. Dùng List.Generate ( tương tự vòng lặp for trong vba ) để duyệt từ 997 xuống mỗi lần trừ 2, nếu true thì gán vào List,
3. Lấy n số từ đầu danh sách bằng List.FirstN
Mã:
let
// thay vong lap FOR
a = List.Generate(
() => 997,
each _ > 100,
each _ - 2,
each if fNguyenTo(_) then _ else null),
// Lay 20 ket qua dau tien
kq = List.FirstN(List.RemoveNulls(a), 20)
in
kqFile đính kèm
Lần chỉnh sửa cuối:
Upvote
0
Góp vui code tìm số nguyên tố
Mã:
Sub xyz()
Dim a(1 To 1000), res(1 To 1000, 1 To 1)
Dim xMin&, xMax&, xU, i&, j&, k&, n&
xMin = 100: xMax = 9999
For i = xMin To 2
n = n + 1: res(n, 1) = i
Next i
'Tao mang cac so nguyen to lam co so so sanh
xU = Int(Sqr(xMax))
For i = 3 To xU Step 2
For j = 1 To k
If i Mod a(j) = 0 Then Exit For
Next j
If j > k Then
k = k + 1: a(k) = i
If i >= xMin Then n = n + 1: res(n, 1) = i
End If
Next i
If n > 0 Then
If xMin < res(n, 1) Then xMin = res(n, 1) + 1
End If
xMin = ((xMin \ 2) * 2 + 1) 'Lay gia tri le
For i = xMin To xMax Step 2
For j = 1 To k
If i Mod a(j) = 0 Then Exit For
Next j
If j > k Then n = n + 1: res(n, 1) = i
Next i
Range("B2").Resize(UBound(res), 1) = res
End Sub
Upvote
0
Định hướng các bước:Có VBA, có Query rồi. Bi giờ ai xung phong viết hàm Lambda hôn?
- Viết thử bằng let
- Tạo dãy số từ 997 xuống 101 (a)
- Tạo dãy số 11 số nguyên tố đầu tiên (nhỏ hơn căn bậc 2 của 997 (b)
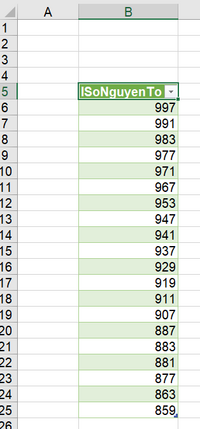
- Tạo ma trận là mod (a, b) (c)
- HStack a và c
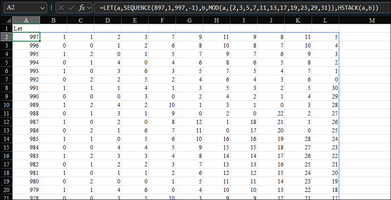
- tìm zero trong từng dòng. Nếu không có con nào thì lấy cột đầu. Bước này chưa tìm được công thức phù hợp, các hàm CountIf, SumIf, lookup, Match chỉ làm việc với range, không làm việc với mảng ảo
- Sort kết quả Descending
- Lấy 10 giá trị đầu tiên.
Nếu làm trên sheet:
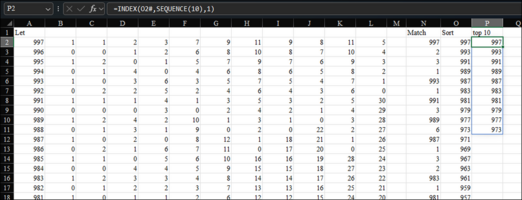
Nhưng chưa làm hoàn toàn bằng 1 công thức duy nhất.
Lần chỉnh sửa cuối:
Upvote
0
Châu Bá Thông
Trí tuệ trong trẻo - nghịch ngợm vô biên
- Tham gia
- 19/12/08
- Bài viết
- 115
- Được thích
- 325
- Nghề nghiệp
- Đốn củi
Thử lại, dùng công thức, không cần VBA hay QueryBa số nguyên tố liên tiếp này bé hơn con số 999 & lớn hơn 100. (đã sửa sau góp ý của các bài 2 - 5)
Chúc các bạn vui vẻ nhân dịp xuân về!
PHP:
=LET(
IsPrime,
LAMBDA(n,
IF(n < 2, FALSE,
IF(n = 2, TRUE,
IF(n = 3, TRUE,
IF(MOD(n, 2) = 0, FALSE,
LET(
maxDiv, SQRT(n),
floorMaxDiv, ROUNDDOWN(maxDiv, 0),
divs, SEQUENCE((floorMaxDiv - 1)/2, 1, 3, 2),
IFERROR(AND(MOD(n, divs) <> 0), TRUE)
)
)
)
)
)
),
nums, SEQUENCE(899, 1, 101, 1),
isPrimeArray, MAP(nums, LAMBDA(x, IsPrime(x))),
primes, FILTER(nums, isPrimeArray),
count, ROWS(primes),
IF(count < 3, "Không tìm thấy bộ ba nào",
HSTACK(
INDEX(primes, SEQUENCE(count - 2)),
INDEX(primes, SEQUENCE(count - 2) + 1),
INDEX(primes, SEQUENCE(count - 2) + 2)
)
)
)
Upvote
0
VetMini
Đang đi tìm hòn đá
- Tham gia
- 21/12/12
- Bài viết
- 17,867
- Được thích
- 24,788
- Nghề nghiệp
- Thầy bói bài ta
Hàm Lambda dùng đệ quy để thay thế vòng lặp.....
Nhưng chưa làm hoàn toàn bằng 1 công thức duy nhất.
Viết hàm VBA đệ quy để xét tính chất nguyên tố. Dựa vào đó mà viết công thức.
Mã:
Function DeQuyNT(ByVal So As Long, Optional Kd As Long = 3) As Boolean
DeQuyNT = False
Select Case So
Case 0, 1: Exit Function
Case 2: DeQuyNT = True: Exit Function
Case Else
If (So And 1) = 0 Then Exit Function
DeQuyNT = True
If Kd > Sqrt(So) Then Exit Function
If So Mod Kd = 0 Then DeQuyNT = False: Exit Function
DeQuyNT = DeQuyNT(So, Kd + 2)
End Select
End Function
Upvote
0
Châu Bá Thông
Trí tuệ trong trẻo - nghịch ngợm vô biên
- Tham gia
- 19/12/08
- Bài viết
- 115
- Được thích
- 325
- Nghề nghiệp
- Đốn củi
TẠO BẢNG 100 SỐ NGUYÊN TỐ GỒM 3 KÝ SỐ LỚN NHẤT.
Thử lấy 50 số nguyên tố lớn nhất trong khoản 100 - 999, sắp xếp theo thứ tự từ lớn đến nhỏ, dùng công thức
PHP:
=SORT(
LET(
IsPrime,
LAMBDA(n,
IF(n < 2, FALSE,
IF(n = 2, TRUE,
IF(n = 3, TRUE,
IF(MOD(n, 2) = 0, FALSE,
LET(
maxDiv, SQRT(n),
floorMaxDiv, ROUNDDOWN(maxDiv, 0),
divs, SEQUENCE((floorMaxDiv - 1)/2, 1, 3, 2),
IFERROR(AND(MOD(n, divs) <> 0), TRUE)
)
)
)
)
)
),
nums, SEQUENCE(900, 1, 100, 1),
isPrimeArray, MAP(nums, LAMBDA(x, IsPrime(x))),
primes, FILTER(nums, isPrimeArray),
top50Primes, INDEX(primes, SEQUENCE(50, 1, ROWS(primes) - 49, 1)),
top50Primes
)
,,-1
)
Lần chỉnh sửa cuối:
Upvote
0
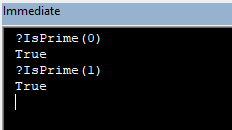
Nếu dùng vùng là từ 0 đến 100 thì sao anh nhỉ ?Function IsPrime(n As Integer) As Boolean Dim i As Integer For i = 2 To Sqr(n) If n Mod i = 0 Then IsPrime = False: Exit Function End If Next i IsPrime = True End Function
Theo định nghĩa thì cần loại 0-1 ra khỏi dãy vì không phải số nguyên tố, nhưng hàm IsPrime vẫn trả về TRUE
Upvote
0
- Tham gia
- 8/6/06
- Bài viết
- 14,776
- Được thích
- 23,229
- Nghề nghiệp
- U80
Copilot:
Bạn đã viết một macro VBA để tìm số hoàn hảo. Đây là cách hoạt động của macro:
Hàm IsPrime(n As Integer): Kiểm tra xem một số n có phải là số nguyên tố hay không.
Nếu n là số nguyên tố, hàm trả về True, ngược lại, trả về False.
Sub TimSoHoanHao():
Tạo một mảng Arr để lưu các số hoàn hảo.
Duyệt qua các giá trị của J từ 2 đến 10.
Kiểm tra nếu J và (2^J)-1 đều là số nguyên tố.
Nếu điều kiện trên đúng, tính số hoàn hảo dựa trên công thức
(2^(J−1))×((2^J−1) và lưu nó vào mảng Arr.
Sau khi hoàn thành, điền các giá trị của mảng Arr vào trang tính "GPE" từ ô A2 trở xuống.
Một số hoàn hảo là một số nguyên dương mà tổng các ước số của nó (trừ bản thân nó) bằng chính nó.
Ví dụ: 6 là số hoàn hảo vì các ước số của nó là 1, 2 và 3, và 1 + 2 + 3 = 6.
[Hãy viết một macro có nội dung như Copilot đã nhìn thấy!]
Bạn đã viết một macro VBA để tìm số hoàn hảo. Đây là cách hoạt động của macro:
Hàm IsPrime(n As Integer): Kiểm tra xem một số n có phải là số nguyên tố hay không.
Nếu n là số nguyên tố, hàm trả về True, ngược lại, trả về False.
Sub TimSoHoanHao():
Tạo một mảng Arr để lưu các số hoàn hảo.
Duyệt qua các giá trị của J từ 2 đến 10.
Kiểm tra nếu J và (2^J)-1 đều là số nguyên tố.
Nếu điều kiện trên đúng, tính số hoàn hảo dựa trên công thức
(2^(J−1))×((2^J−1) và lưu nó vào mảng Arr.
Sau khi hoàn thành, điền các giá trị của mảng Arr vào trang tính "GPE" từ ô A2 trở xuống.
Một số hoàn hảo là một số nguyên dương mà tổng các ước số của nó (trừ bản thân nó) bằng chính nó.
Ví dụ: 6 là số hoàn hảo vì các ước số của nó là 1, 2 và 3, và 1 + 2 + 3 = 6.
[Hãy viết một macro có nội dung như Copilot đã nhìn thấy!]
Lần chỉnh sửa cuối:
Upvote
0
Em cũng hay coi video từ kênh: https://www.youtube.com/c/ToánThúVịSub TimSoHoanHao():
Video về số hoàn hảo
Anh xem, thấy kênh cũng có nhiều điều thú vị.
Upvote
0
VetMini
Đang đi tìm hòn đá
- Tham gia
- 21/12/12
- Bài viết
- 17,867
- Được thích
- 24,788
- Nghề nghiệp
- Thầy bói bài ta
Viết 1 hàm Lambda đệ quy cũng được, nhưng không hiệu quả lắm. Con toán xét Nguyên Tố có một vài công việc ưu hóa cho nên nếu đệ quy thì những công việc này cứ phải lặp lại.
Dùng 2 hàm, một hàm dọn trước, sau đó mới gọi hàm chia thử (đệ quy)
Name SoNTchiaThu
=Lambda(x, y, z, If(z > y, True, If(Mod(x, z)=0, False, SoNTchiaThu(x, y, z+2))))
Name SoNT
=Lambda(x, Switch(x, 0, False, 1, False, 2, True, If(IsEven(x), False, SoNTchiaThu(x, Trunc(Sqrt(x)), 3)))
Sử dụng: =SoNT(số)
Dùng 2 hàm, một hàm dọn trước, sau đó mới gọi hàm chia thử (đệ quy)
Name SoNTchiaThu
=Lambda(x, y, z, If(z > y, True, If(Mod(x, z)=0, False, SoNTchiaThu(x, y, z+2))))
Name SoNT
=Lambda(x, Switch(x, 0, False, 1, False, 2, True, If(IsEven(x), False, SoNTchiaThu(x, Trunc(Sqrt(x)), 3)))
Sử dụng: =SoNT(số)
Upvote
0
Bài viết mới nhất
- Trả lời
- 0
- Đọc
- 90
hướng dẫn xóa dòng, cột file excel
(1 người xem)
- Trả lời
- 1
- Đọc
- 55
- Trả lời
- 4
- Đọc
- 163
- Trả lời
- 0
- Đọc
- 39
- Trả lời
- 20
- Đọc
- 539
- Trả lời
- 13
- Đọc
- 315
- Trả lời
- 2
- Đọc
- 250
- Trả lời
- 11
- Đọc
- 942
- Trả lời
- 18
- Đọc
- 7K
- Trả lời
- 0
- Đọc
- 35
- Trả lời
- 17
- Đọc
- 442
- Trả lời
- 7
- Đọc
- 243
- Trả lời
- 5
- Đọc
- 172
- Trả lời
- 3
- Đọc
- 138
- Trả lời
- 5
- Đọc
- 360
- Trả lời
- 12
- Đọc
- 955
- Đã giải quyết
- Trả lời
- 92
- Đọc
- 27K
Thành viên có số lượng bài viết cao nhất tháng
- Maika8008 39
- thanthanhan 23
- dungpham01 19
- ongke0711 19
- ptm0412 17
- eagle12 16
- nguyenanhtruong2409 16
- Phan Thế Hiệp 16
- HUONGHCKT 12
- vic_it 11
- nhhnam 10
- pycckuu410 10
- dieppk.nb92 10
- Vũ Hải Sơn 9
- HeSanbi 9
- Gà Con yêu VBA 8
- bsbnhh 7
- duongnhuxuyen 7
- Hana2610 6
- kaoehtkid 6
Thành viên có điểm tương tác cao nhất tháng
- Phan Thế Hiệp 82
- Maika8008 32
- thanthanhan 20
- ongke0711 17
- ptm0412 17
- HeSanbi 15
- dungpham01 11
- eagle12 9
- HUONGHCKT 9
- Cúc Hr 8
- dieppk.nb92 6
- Mr.hieudoanxd 5
- befaint 5
- pycckuu410 5
- SA_DQ 5
- Hoàng Tuấn 868 4
- Phuocam 4
- nguyenanhtruong2409 4
- nhhnam 2
- Gà Con yêu VBA 2