Bài tập về lựa chọn phương án tối ưu

[kittenkid]

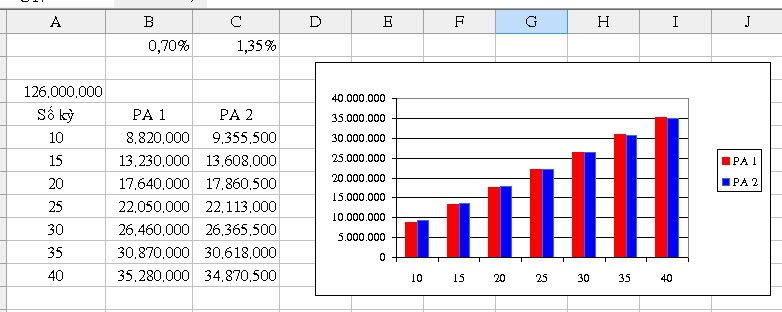
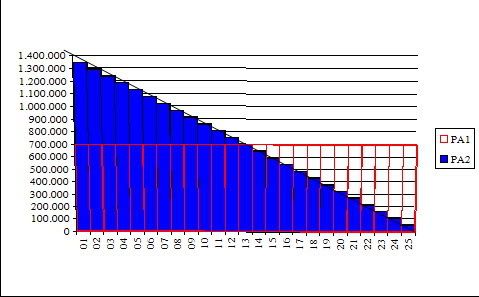
Một người vay ngân hàng 100 triệu , ngân hàng có 2 phương án:
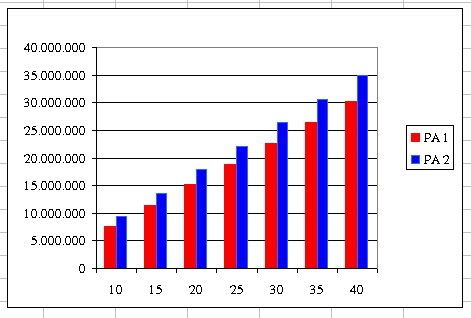
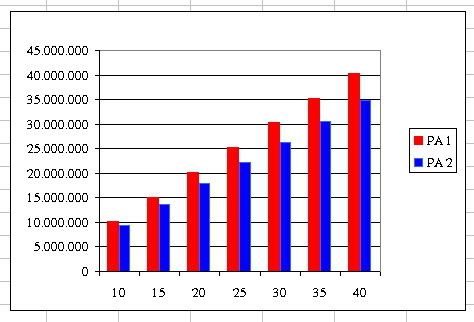
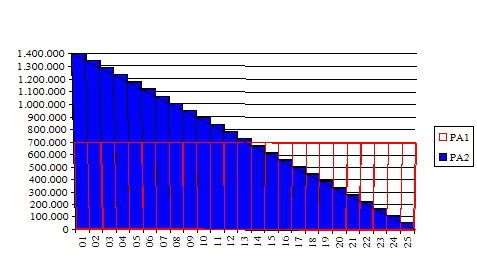
-Phương án 1:thu lãi hàng tháng đều nhau với số tiên trả gốc 4 triệu cồng với tiền lãi bằng số tiền vay nhân với lãi suất 0.7%
Phương án 2:thu lãi giảm dần hàng tháng với số tiền trả gốc 4 triệu cộng với số dư nợ còn lại nhân với lãi suất 1.35%
Ngân hàng nên chọn phương án nào ?Tính tổng lãi, Lãi suất thực của từng phương án,
Bài này minh làm sao thế?Lựa chọn của ngân hàng và lựa chọn của người vay vốn khác nhau như thế nào?

 

[kongcom]

Phương án 1 : Ngân hàng thu về 8.400.000 Đ lãi thực
Phương án 2 : Tổng lãi thu về cho Ngân hàng là :6.264.678.Đ

Vậy Phương án 2 Khách hàng có lợi hơn bạn à .

 

[kittenkid]

không phải, ở đây là lựa chọn cho ngân hàng chứ không phải cho khách hàng. Nếu cho ngân hàng thì lựa chọn phương án 1 phải không?

 

[kittenkid]

ah mình ghi thiếu đề , phải thêm là trong vòng 25 tháng nữa. Nhưng mà bạn tính sao vậy ?chỉ mình đi.

 

[kongcom]

Bạn nên gộp bài lại cho gọn .
Thêm 25 tháng là sao ? Toán tỷ lệ thuận thôi mà ? Thời hạn vay càng dài thì người vay càng tốn nhiêù tiền trả lãi . Trong trường hợp nào thì phương án 1 ngân hàng cũng lợi nhiều hơn .
Cách tính , bạn có thể tham khảo tại topic " Sai lầm khi vay tiền tại ngân hàng " . Trong đó tôi có gửi file công cụ lên rồi .

 

[kittenkid]

mình có đọc bài về "sai lầm khi vay tiền tại ngân hàng" rồi , nhưng mình chưa học về cách dùng những hàm đó, mình chỉ mới học về rate, IRR thôi. mình ko biết tại sao mình sử dụng hàm IRR như thế nào mà cứ bị ghi là DIV/0!Mình ko biết sai chỗ nào nữa!bạn giải bài tập này theo hàm IRR sao, chỉ mình với.

 

[ptm0412]

Bài này chả có dùng hàm tài chính hay hàm hạng bét nào của Excel cả:
1. Phương án 1: Trả gốc bằng nhau, lãi bằng nhau 25 kỳ:
- Gốc: 4.000.000 x 25 =100.000.000
- Lãi: 100.000.000 x 0,7%*25 = 17.500.000

2. Phương án 2: Trà gốc bằng nhau, lãi giảm dần 25 kỳ:
- Gốc: 4.000.000 x 25 =100.000.000
- Lãi: (100.000.000 + 96.000.000 + 92.000.000 + 88.000.000 + . . . +4.000.000) x 1.35%
= [(100.000.000 + 4.000.000) x 25 / 2 ] x 1.35% = 17.550.000

(Công thức tính tổng một cấp số cộng, 25 số hạng, công sai = - 4 triệu).

 

[ptm0412]

Phân tích lại 2 phương án cho vay

TO KongCom

Trong trường hợp nào thì phương án 1 ngân hàng cũng lợi nhiều hơn .

Câu phát biểu của bạn chưa chính xác. Phương án nào có lợi hơn tuỳ thuộc vào so sánh giữa lãi suất thực của 2 phương án. Trong thí dụ này, - lãi suất thực của phương án 1 là:
=RATE(25;-4.700.000;100.000.000;0;0;1,25%) = 1,28%
- Lãi suất thực của Phương án 2 là 1,35%
Vả trong thí dụ này, lãi suất thực của PA 1 suýt soát bằng LS thực của PA 2. Khi thời gian kéo dài ta có đồ thị sau: (cái này mới là Excel)

Ta thấy PA1 ban đầu nhỏ hơn PA2, sau đó đuổi kịp và cao hơn PA2.

Tuy nhiên phân tích lại công thức tính lãi phải trả của PA 1:
Lãi = khoản vay x lãi suất x số kỳ trả lãi
khi khoản vay không đổi, đây là 1 hàm tuyến tính, hệ số là lãi suất, biến thiên theo số kỳ trả. Khi lãi suất càng cao thì độ dốc của đường biểu diễn PA1 sẽ càng cao và ngược lại.

So với lãi suất thực của PA2, với độ dốc thấp, PA1 sẽ không lên kịp PA2 và chả bao giờ bằng P2. Thí dụ với lãi suất của PA 1 là 0,6%:

Ngược lại, với độ dốc cao, PA1 nhanh chóng vượt qua PA2 thậm chí ở mức cao hơn hẳn: Thí dụ với lãi suất của PA1 là 0,8%:

Bạn thấy không?

 

[kongcom]

Phân tích của PTM0412 rất hay . Bạn đưa bài toán này trở nên khá tổng quát và minh họa cũng sinh động .

Nhưng theo mình những phân tích của bài toán này chỉ dựa trên một tài khoản vay duy nhất nên chưa thấy được hết những lợi ích mà phương án 1 mang lại cho ngân hàng .

Ở PA2 : tiền về tới ngân hàng thì ngân hàng ngưng hưởng lãi . Mặc dù lãi xuất là gần gấp đôi so với PA1 . nhưng lãi thực do số tiền này mang về cho ngân hàng là duy nhất . -----> Đường đồ thị cho chúng ta là dạng tam giác vuông

Ở PA1 : Hàng tháng số dư giảm bao nhiêu thì ngân hàng vẫn hưởng lãi xuất trên 100% số tiền cho vay ban đầu . -------> Đồ thị cho chúng ta là hình chữ nhật mà chiều dài đáy bằng một cạnh vuông tam giác vuông trên.

Nếu tỷ lệ thỏa đáng , diện tích hai hình trên phải bằng nhau do vậy chiều cao của tam giác phải gấp 2 lần chiều cao hình chữ nhật . Nghĩa là lãi xuất cho PA2 phải bằng 1,4% thì ngân hàng mới thu lợi tương đương với PA1 được .

Phân tích tối ưu thì ta phải tìm ra tỷ lệ nào là có lợi hơn trong tất cả các trường hợp chứ không phải tỷ lệ mà đúng trong trường hợp này nhưng sai trong trường hợp khác phải không nhỉ ?

 

[ptm0412]

Phân tích tối ưu thì ta phải tìm ra tỷ lệ nào là có lợi hơn trong tất cả các trường hợp chứ không phải tỷ lệ mà đúng trong trường hợp này nhưng sai trong trường hợp khác phải không nhỉ ?

Trong bài tập này phương án tối ưu đã rõ (xem bài #7 của tớ).


Còn để đúng trong mọi trường hợp, tỷ lệ giữa 2 lãi suất không phải là 2 như bạn tính.

Nghĩa là lãi xuất cho PA2 phải bằng 1,4% thì ngân hàng mới thu lợi tương đương với PA1 được .

Lý luận của bạn dựa trên Diện tích hình tam giác bằng diện tích hình chữ nhật, chiều cao tam giác bằng 2 lần chiều rộng hình chữ nhật, suy ra r2 =2 r1 = 1,4% ?
nhưng bạn đã thử kết quả đó chưa? Mình thử thì thấy không đúng.
Mình cho rằng r2 của phương án 2 phải bằng lãi suất thực của phương án 1: =RATE(25;-4.700.000;100.000.000;0;0;1,25%) = 1,28%, nhưng khi kiểm tra thì cũng không đúng.
Rốt cuộc tính bằng solver thì cho 1,346154%
Vậy cách tính như thế nào cho đúng thì mình vẫn chưa biết.
Chỉ có thể so sánh tìm tối ưu cho trường hợp cụ thể thôi.

 

[kongcom]

Sai thứ nhất : Phương án 2 , kì đầu khách phải thanh toán lãi cho số dư còn lại nghiã là 96000000Đ chứ không phải là 100000000Đ------> Các bạn hãy đọc kĩ và hiểu đề bài thì sẽ thấy

Do vậy dẫn tới tổng số tiền lãi mà khách phải trả là 16200000Đ thấp hơn nhiều so với tính toán của bạn

Sai thứ hai khi bạn mặc nhiên công nhận dữ liệu là đã tối ưu , bạn hãy cho hàm số này trượt trên các tỷ lệ khác nhau ngẫu nhiên

Sai thứ ba khi chúng ta hiểu rằng 25 lần trả tiền lãi thì PA1 khách hàng chỉ chịu lãi có 25 tháng , vì sau thời gian đó thì đã có 26 tháng trôi qua . Trên thực tế , 25 tháng vay thì khách tới trả lãi có 24 lần

Còn nếu cùng một cách trã lãi theo 24 kì thì khách chỉ phải trã 16800000Đ theo phương án 1 Theo con số này thì cũng tương đương với lãi xuất 1,4 phần trăm theo phương án 2 .

 

[ptm0412]

Tôi đã xem file của bạn. Thế bạn trả gốc theo đề bài như thế nào?
Đề bài:

Phương án 1:thu lãi hàng tháng đều nhau với số tiên trả gốc 4 triệu cồng với tiền lãi bằng số tiền vay nhân với lãi suất 0.7%
Phương án 2:thu lãi giảm dần hàng tháng với số tiền trả gốc 4 triệu cộng với số dư nợ còn lại nhân với lãi suất 1.35%

bạn có 3 cái sai:
1. Nếu bạn trả lãi 24 lần cộng với gốc 4 triệu x 24 lần =96 triệu, chưa hết nợ mà?

2. Bạn vay ngày 01/01/08, số tiền vay 100.000.000, đến ngày 01/02/08 trả tiền lần 1, vậy lãi tính trên dư nợ 100 triệu hay 96 triệu? Chả lẽ từ 01/01 đến 01/02, ngân hàng để bạn xài 4 triệu không tính lãi à? (dù với bất kỳ PA nào)

3. Theo bạn thì khi trả tiền lần 25 là đã 26 tháng trôi qua, vậy ngày 01/02/08 trả tiền lần 1 thì mấy tháng đã trôi qua?

4. Tôi không cho rằng dữ liệu là tối ưu. Tôi chỉ cho rằng trong đề bài cụ thể này, ngân hàng sẽ chọn PA nào. Còn tôi cho số liệu trượt là để phân tích khi kéo dài thời gian theo nguyên văn của bạn:

Thời hạn vay càng dài thì người vay càng tốn nhiêù tiền trả lãi . Trong trường hợp nào thì phương án 1 ngân hàng cũng lợi nhiều hơn

Tôi đã phân tích rằng với lãi suất không đổi theo đề bài, chọn số tiền vay là 126 triệu (vì 126 tr là bội số của 10, 15, 20, 25, 30, 35, 40) thì:
khi số kỳ trả là 10, 15, 20, 25 số tiền lãi phải trả của PA1 là ít hơn PA1, đến khi số kỳ trả 30, 35, 40 số tiền lãi phải trả của PA1 mới nhiều hơn.
Sau đó tôi phân tích khi lãi suất PA 1 giảm hoặc tăng thì so sánh 2 con số tổng lãi phải trả của 2 phương án sẽ như thế nào. Tôi cũng không phải là chọn số ngẫu nhiên: 0,6% là cận dưới, 0,8% là cận trên của 0,7%.
Nếu suy luận rộng thêm thì tại 1 điểm nào đó của lãi suất (khoảng trên 0,7 nhưng dưới 0,8%, độ dốc của 2 hàm số bằng nhau, và 2 đường sẽ trùng nhau.

Cảm phiền bạn xem lại.

 

[ptm0412]

Đã tìm ra công thức tính

Từ công thức tính ở bài #7:
- Lãi PA1 = PV x r1 x n
- Lãi PA2 = (PV + PV/n) x n/2 x r2
Với PV là khoản vay, r1 là lãi suất PA1, n là số kỳ trả, r2 là lãi suất PA2.
Giải phương trình PA1 = PA2 ta được:
r2 = r1 x 2 x n/ (n + 1)

Đó là công thức tổng quát so sánh tổng lãi của 2 cách tính lãi vay:
- Cách 1: Trả gốc bằng nhau, lãi bằng nhau (tính trên tổng nợ) trong n kỳ
- Cách 2: Trả gốc bằng nhau, lãi theo dư nợ giảm dần cũng trong n kỳ

Nếu r2 < r1 x 2 x n/ (n + 1), tổng lãi PA1 < tổng lãi PA2
Nếu r2 > r1 x 2 x n/ (n + 1), tổng lãi PA1 > tổng lãi PA2

Cụ thể trong bài tập này, tổng lãi 2 phương án bằng nhau khi r2 = r1 x 25 x 2 /26 = 0,7% x 25/13 = 1,34615%
Đúng bằng cách tính của solver ở bài #10

Trừ khi bạn Kongcom có ý kiến khác.

 

[ptm0412]

Giải thích thêm

Trong lý luận của bạn Kongcom về diện tích hình tam giác và hình chữ nhật, có 1 chút nhầm lẫn như sau:
_ PA1: hình chữ nhật: đúng
- PA2: hình tam giác: thực ra là tổng những hình chữ nhật đứng kế tiếp nhau.
Nếu r2 = 2 x r1 = 2 x0,7% = 1,4% ta có hình minh họa như sau:

ta thấy tổng diện tích màu xanh lớn hơn diện tích hình tam giác 1 tí tẹo.
Tính thử cái tí tẹo đó: gồm 25 hình tam giác, mỗi hình có:
đáy = 1,
cao = 1/25 của chiều cao cột đầu tiên (theo tỷ lệ tam giác đồng dạng) = PV x r2/25
Tổng diện tích các hình tam giác nhỏ:
= 25 x 1/2 x 1 x PV x r2/25
= PV/2 x r2
= 100.000.000/2 x 1,4% =700.000

Kiểm tra lại bằng cách so sánh tổng PA1 và PA2:
PA2 - PA1 = 18.200.000 - 17.500.000 = 700.000 (Đúng)

Nếu muốn tổng diện tích màu xanh bằng tổng diện tích màu đỏ, cột đầu tiên của PA2 phải thấp hơn 1.400.000 1 tí teo.

Ta thấy bằng hình học thì tổng diện tích màu xanh bằng với tổng diện tích màu đỏ, chiều cao cột xanh đầu tiên thấp hơn 1.400.000. Cụ thể bằng 1.346.154 theo đồ thị, và bằng PV x 1,346154% theo kết quả giải phương trình bài trước.

Ngoài ra lấy hơn bù kém, lấy nhô ra bù thụt vào, diện tích màu xanh bằng diện tích hình tam giác (0; 1.400.000; 25) và bằng diện tích hình chữ nhật 25 x 700.000.

 

[alonelovelove89]

Để tính lãi thực , bạn có thể dùng hàm effect (mình ko cắhhcc chắn lắm, tại cái này là do mình đọc 1 số tài liệu nó nói vậy đó)^^.
Còn về bài toán đó, bạn xem trong file đính kèm của mình!